Question

Write the equation for the parabola and draw the graph
Vertex$\left( {0,1} \right)$, focus $\left( {0,5} \right)$

Answer 1

Hint: - We proceed our solution with the Standard equation of parabola ${\left( {x - h} \right)^2} = 4a\left( {y - k} \right)$. With vertex$\left( {h,k} \right)$, focus$\left( {0,a} \right)$.

Complete step-by-step solution -
Given data:
Vertex$\left( {0,1} \right)$, focus $\left( {0,5} \right)$
So, on comparing
$h = 0,{\text{ }}k = 1,{\text{ }}a = 5$
And the parabola is vertically upward
So, the equation of parabola becomes

$$\Rightarrow {\left( {x - 0} \right)^2} = 4 \times 5\left( {y - 1} \right) \\\ \Rightarrow {x^2} = 20\left( {y - 1} \right)............\left( 1 \right) \\\$$

Equation of directrix is written as $\left( {y - 1} \right) = - a$

$$\Rightarrow y - 1 = - 5 \\\ \Rightarrow y = - 4.............\left( 2 \right) \\\$$

So, equation (1) is the required equation of parabola and equation (2) is the equation of directrix of the parabola.
Diagram of the parabola is shown below,

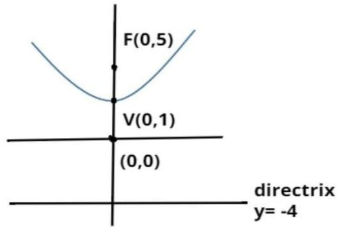
Note:- In such types of questions always remember the standard equation of the parabola, then compare the coordinates of vertex and focus and substitute that in the standard equation, then calculate the equation of the directrix, then draw the diagram of the parabola as shown above.