Question

Write the Arrhenius equation. Derive an expression for temperature variation.

Answer 1

Arrhenius deduced his expression in which he related the rate of the reaction to the effect of temperature which is known as The Arrhenius equation. This equation can be modified into a log form when two temperatures are given.

Complete step by step answer:
Arrhenius deduced his expression in which he related the rate of the reaction to the effect of temperature which is known as The Arrhenius equation.
The equation called the Arrhenius equation is usually written as $k=A{{e}^{-{{E}_{a}}/RT}}$ where the pre-exponential factor A is a constant and is called frequency factor and ${{E}_{a}}$ is called the activation energy, R is the gas constant and T is the temperature.
When we take logarithm on both sides, we get
$\ln k=\ln A-\dfrac{{{E}_{a}}}{RT}$

If the values of the rate constant at temperature ${{T}_{2}}$ and ${{T}_{1}}$ are ${{k}_{2}}$ and ${{k}_{1}}$ respectively, then we have,
$\ln {{k}_{2}}=\ln A-\dfrac{{{E}_{a}}}{R{{T}_{2}}}$
$\ln {{k}_{1}}=\ln A-\dfrac{{{E}_{a}}}{R{{T}_{1}}}$
So, subtracting the above equations, we get:
$\ln {{k}_{2}}-\ln {{k}_{1}}=-\dfrac{{{E}_{a}}}{R{{T}_{2}}}-\dfrac{{{E}_{a}}}{R{{T}_{1}}}=\dfrac{{{E}_{a}}}{R{{T}_{1}}}-\dfrac{{{E}_{a}}}{R{{T}_{2}}}$

Or we can write,
$\ln \dfrac{{{k}_{2}}}{{{k}_{1}}}=\dfrac{{{E}_{a}}}{R}\left[ \dfrac{{{T}_{2}}-{{T}_{1}}}{{{T}_{2}}{{T}_{1}}} \right]$

And its log form is:
$\log \dfrac{{{k}_{2}}}{{{k}_{1}}}=\dfrac{{{E}_{a}}}{2.303R}\left[ \dfrac{{{T}_{2}}-{{T}_{1}}}{{{T}_{2}}{{T}_{1}}} \right]$
To test the validity of the Arrhenius equation, let us consider the equation as:

$\ln k=-\dfrac{{{E}_{a}}}{RT}+\ln A$
Or it can be converted into:
$\log k=-\dfrac{{{E}_{a}}}{2.303RT}+\log A$
This equation can be written in the form of the equation of the straight line.
The equation of the straight line is: $y=mx\text{ + }c$

So, in the straight line equation, when we plot a graph between y and x, we get m as the slop.
Similarly when we plot the graph for the equation $\log k=-\dfrac{{{E}_{a}}}{2.303RT}+\log A$:
$\log k$ is the y and $\dfrac{1}{T}$ is the x, the validity of the equation is confirmed.
So, when we plot the graph we get m = $\dfrac{-{{E}_{a}}}{2.303R}$
So, the slope of the line = $\dfrac{-{{E}_{a}}}{2.303R}$
The graph of log k vs $\dfrac{1}{T}$ is given below:

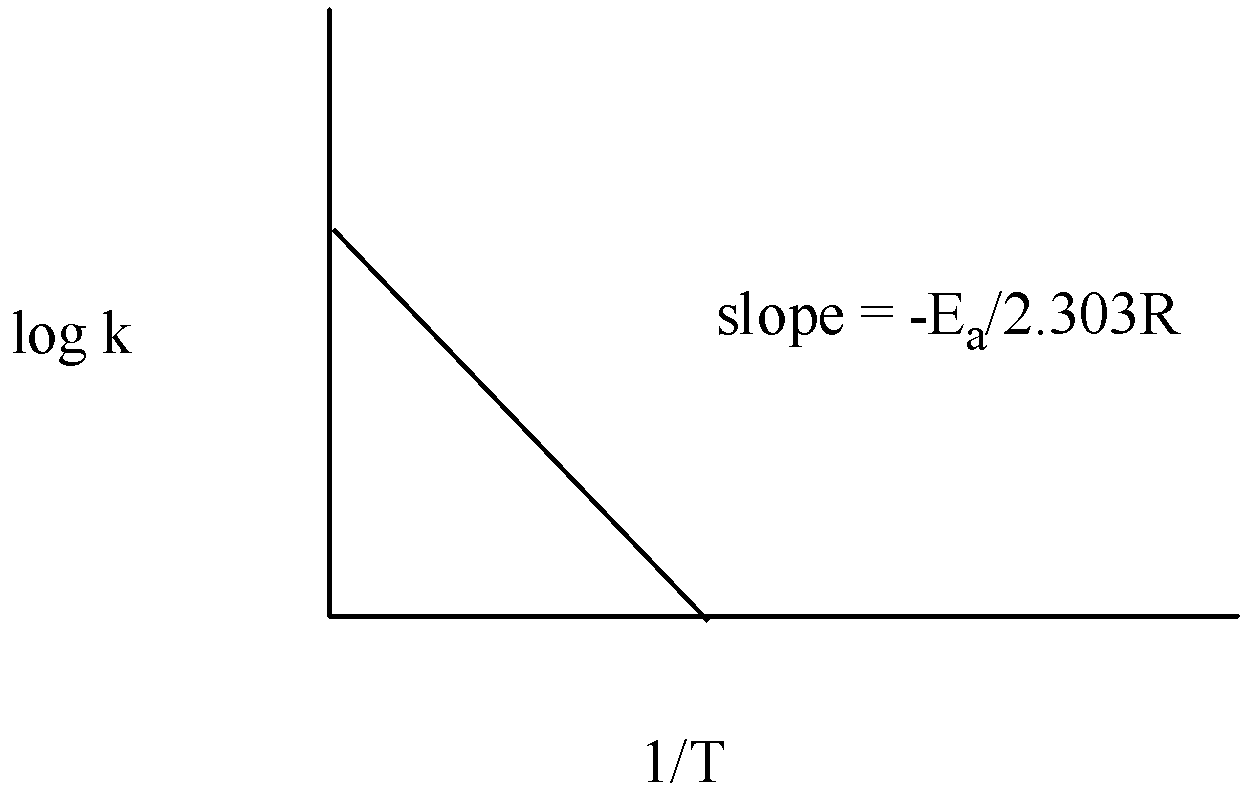
Thus, measuring the slope of the line, the value of ${{E}_{a}}$ can be calculated.

Note: If we plot a straight line graph for the equation$\ln k=-\dfrac{{{E}_{a}}}{RT}+\ln A$, the y will be ln k and the x will be $\dfrac{1}{T}$ so in this case, we get the slope of$-\dfrac{{{E}_{a}}}{R}$. So, by converting any equation to the straight-line equation we can find the slope of the equation.