Question

Write the amplitude and modulus of $- 4 - 4i$.

Answer 1

Hint: To find the amplitude of the given complex number, we will use the formula,
$Amp\left( z \right) = \pm {\tan ^{ - 1}}\left| {\left( {\dfrac{b}{a}} \right)} \right| \pm \pi /0$
To find the modulus of the given complex number, we will use the following formula:
$\left| z \right| = \sqrt {{a^2} + {b^2}}$
These formulas are for $z = a + ib$

Complete step-by-step solution -
Before calculating the amplitude and modulus of a given complex number, we must first know what these terms are. A complex number $a + ib$ can be represented in the form of $z = \left( {a + ib} \right) = r\left( {\cos \theta + i\sin \theta } \right)$ , where $r > 0$ , here $\theta$ is the amplitude of the complex number. Alternatively, $\theta$ can also be calculated from the formula shown below:
$Amp\left( z \right) = \theta = \pm {\tan ^{ - 1}}\left| {\left( {\dfrac{b}{a}} \right)} \right| \pm \pi /0$
The sign will depend on the quadrant in which this complex number is present. So now ,first we will plot the complex number roughly in the complex plane.

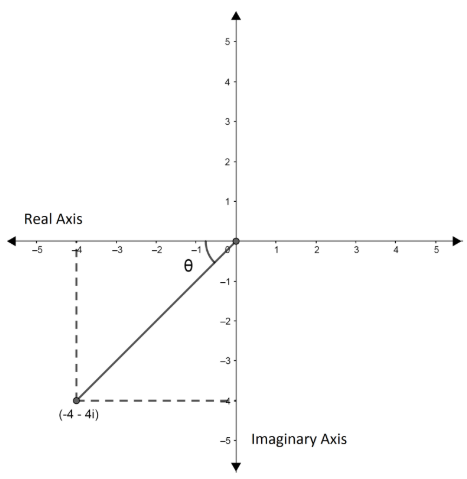
Here, we can see that the complex number is present in the third quadrant. Thus, the amplitude of the complex number will be given by:
$\theta = Amp\left( z \right) = {\tan ^{ - 1}}\left| {\dfrac{b}{a}} \right| - \pi$
$\Rightarrow Amp\left( z \right) = {\tan ^{ - 1}}\left| {\dfrac{{ - 4}}{{ - 4}}} \right| - \pi$
$\Rightarrow Amp\left( z \right) = {\tan ^{ - 1}}\left( 1 \right) - \pi$
$\Rightarrow Amp\left( z \right) = \dfrac{\pi }{4} - \pi$
$\Rightarrow Amp\left( z \right) = \dfrac{{ - 3\pi }}{4}$
Now, we will calculate the modulus of the given complex number. The modulus of the complex number $z = a + ib$ is represented by $\left| z \right|$ and can be calculated by the formula:
$\left| z \right| = \sqrt {{a^2} + {b^2}}$
$\Rightarrow \left| z \right| = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 4} \right)}^2}}$
$\Rightarrow \left| z \right| = \sqrt {16 + 16}$
$\Rightarrow \left| z \right| = \sqrt {32}$
$\Rightarrow \left| z \right| = 4\sqrt 2$
So, the amplitude of the complex number $\left( { - 4 - 4i} \right) = \dfrac{{ - 3\pi }}{4}$ and the modulus of $- 4 - 4i = 4\sqrt 2$.

Note: In the question, we have to calculate the amplitude not the argument of complex function. There is a slight difference between the both. The range of amplitude is $\left( { - \pi ,\pi } \right]$ and the range of arrangement is $\left[ {0,2\pi } \right)$ . Also, we can calculate the amplitude of every complex number except 0.The amplitude of 0 does not exist. Also, in the formula $Amp\left( z \right) = \pm {\tan ^{ - 1}}\left| {\left( {\dfrac{b}{a}} \right)} \right| \pm \pi /0$ and $\left| z \right| = \sqrt {{a^2} + {b^2}}$ , a and b both should be real numbers. If they are complex, then the above formulas are not valid.