Question
Question: Write down the components of four forces \( {\vec F_1} \) , \( {\vec F_2} \) , \( {\vec F_3} \) and ...
Write down the components of four forces F1 , F2 , F3 and F4 along ox and oy directions as shown in the figure.
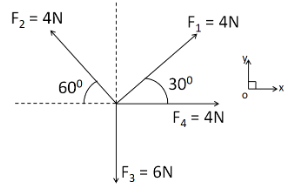
Solution
Hint : To solve this question, we have to consider the inclination angle of all the forces with reference to the ox direction. The component along ox will be obtained by multiplying cosine of the inclination, and that along oy will be obtained after multiplying sine of the inclination with the magnitude of the force.
Complete step by step answer
As we have to take the components of the forces along ox and oy directions, so we take these directions positively.
Now, for the first force F1 :
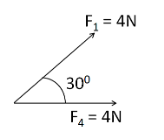
The magnitude of F1 is equal to 4N
Therefore, the component of F1 along ox is
F1ox=4cos30∘
⇒F1ox=23N
And the component f F1 along oy is
F1oy=4sin30∘
⇒F1oy=2N
For the second force F2 :
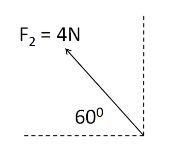
The magnitude of F2 is equal to 4N
Therefore, the component of F2 along ox is
F2ox=−4cos60∘
⇒F2ox=−2N
And the component f F1 along oy is
F2oy=4sin60∘
⇒F2oy=23N
For the third force F3 :
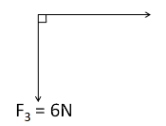
The magnitude of F3 is equal to 6N .
Therefore, the component of F3 along ox is
F3ox=6cos90∘
⇒F3ox=0N
And the component f F3 along oy is
F3oy=−6sin90∘
⇒F3oy=−6N
For the fourth force F4 :
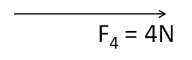
The magnitude of F4 is equal to 4N .
Therefore, the component of F3 along ox is
F4ox=4cos0∘
⇒F4ox=4N
And the component f F3 along oy is
F4oy=4sin0∘
⇒F4oy=0N .
Note
We need to take proper care of the positive and the negative signs of the forces while writing the components. For this, it is always convenient to choose the reference positive direction of the x and the y axis as we have chosen in the above solution. We could also consider the angles of all the forces with the ox directions, to mathematically get the correct signs of the components.
