Question

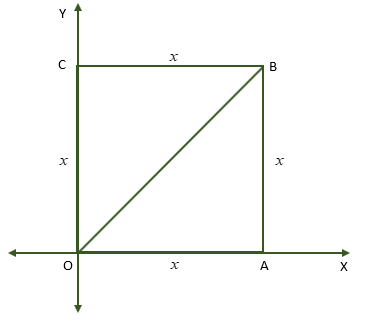
Write down the $2 \times 2$ matrix $A$ which corresponds to a counter-clockwise rotation of $60^\circ$ about the origin. In the diagram, the square $OABC$ has its diagonal of $2\sqrt 2$ units in length. The square is rotated counterclockwise about $60^\circ$ through $O$. Find the coordinates of the vertices of $C$ after rotating.
If the coordinates are $\left( {a,b} \right)$, find the value of ${a^2} + {b^2}$.

Answer 1

Here, we will use the concept of a rotation matrix to write the $2 \times 2$ matrix $A$ which corresponds to a counter-clockwise rotation of $60^\circ$ about the origin. We will use Pythagoras’s theorem to get the length of the sides of the square. The length of the side of the square can be used to find the coordinates of point $C$ before rotation. Finally, we will use the rotation matrix and the coordinates of $C$ to find the coordinates of $C$ after rotation.

Complete step by step solution:
A rotation matrix is a $2 \times 2$ matrix which rotates the points in the Cartesian plane in a counter-clockwise manner through an angle of $\theta$ about the origin.
The rotation matrix is given by \left[ {\begin{array}{*{20}{c}}{\cos \theta }&{ - \sin \theta }\\\\{\sin \theta }&{\cos \theta }\end{array}} \right].
We can substitute $\theta = 60^\circ$ to get the $2 \times 2$ matrix $A$ which corresponds to a counter-clockwise rotation of $60^\circ$ about the origin.
Thus, we get the matrix $A$ as
\begin{array}{c}A = \left[ {\begin{array}{*{20}{c}}{\cos 60^\circ }&{ - \sin 60^\circ }\\\\{\sin 60^\circ }&{\cos 60^\circ }\end{array}} \right]\\\ = \left[ {\begin{array}{*{20}{c}}{\dfrac{1}{2}}&{ - \dfrac{{\sqrt 3 }}{2}}\\\\{\dfrac{{\sqrt 3 }}{2}}&{\dfrac{1}{2}}\end{array}} \right]\end{array}
Now, we know that all sides of a square are equal. Let the sides of the square be equal to $x$ units.
The triangle $OAB$ is a right-angled triangle because all angles in a square are right angles.
Pythagoras’s theorem states that the square of the hypotenuse is equal to the sum of the square of the base and the square of the perpendicular.
We will apply Pythagoras’s theorem in triangle $OAB$ to get the value of $x$, that is the length of the side of the square.
Thus, we get

\Rightarrow {x^2} + {x^2} = {\left( {2\sqrt 2 } \right)^2}\\\ \Rightarrow 2{x^2} = 8\\\ \Rightarrow {x^2} = 4\\\ \Rightarrow x = \sqrt 4 \\\ \Rightarrow x = \pm 2 $$ Thus, the length of the side of the square is 2 units (length cannot be negative). Therefore, the coordinates of point $$C$$ before rotation are $$\left( {0,2} \right)$$. Now, to rotate a point $$\left( {x,y} \right)$$ counter-clockwise through an angle of $$\theta $$ about the origin, we multiply the matrix $$\left[ {\begin{array}{*{20}{c}}{\cos \theta }&{ - \sin \theta }\\\\{\sin \theta }&{\cos \theta }\end{array}} \right]$$ by $$\left[ {\begin{array}{*{20}{c}}x\\\y\end{array}} \right]$$. Let the coordinates of point $$C$$ after rotation be $$\left( {a,b} \right)$$. To rotate the point $$C\left( {0,2} \right)$$ counter-clockwise through an angle of $$60^\circ $$ about the origin, we will multiply the rotation matrix $$A = \left[ {\begin{array}{*{20}{c}}{\dfrac{1}{2}}&{ - \dfrac{{\sqrt 3 }}{2}}\\\\{\dfrac{{\sqrt 3 }}{2}}&{\dfrac{1}{2}}\end{array}} \right]$$ by $$\left[ {\begin{array}{*{20}{c}}0\\\2\end{array}} \right]$$. Thus, we get $$\begin{array}{c}\left[ {\begin{array}{*{20}{c}}a\\\b\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\dfrac{1}{2}}&{ - \dfrac{{\sqrt 3 }}{2}}\\\\{\dfrac{{\sqrt 3 }}{2}}&{\dfrac{1}{2}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}0\\\2\end{array}} \right]\\\ = \left[ {\begin{array}{*{20}{c}}{\left( {\dfrac{1}{2} \times 0} \right) + \left( { - \dfrac{{\sqrt 3 }}{2} \times 2} \right)}\\\\{\left( {\dfrac{{\sqrt 3 }}{2} \times 0} \right) + \left( {\dfrac{1}{2} \times 2} \right)}\end{array}} \right]\\\ = \left[ {\begin{array}{*{20}{c}}{ - \sqrt 3 }\\\1\end{array}} \right]\end{array}$$ Hence, the coordinates of the point $$C$$ after rotation are $$\left( { - \sqrt 3 ,1} \right)$$ counter-clockwise about $$60^\circ $$ through $$O$$. Comparing $$\left( {a,b} \right)$$ and $$\left( { - \sqrt 3 ,1} \right)$$, we get $$a = - \sqrt 3 $$ and $$b = 1$$. We will substitute these values to find the value of the expression $${a^2} + {b^2}$$, that is $$\begin{array}{c}{a^2} + {b^2} = {\left( { - \sqrt 3 } \right)^2} + {1^2}\\\ = 3 + 1\\\ = 4\end{array}$$ Thus, the value of the expression $${a^2} + {b^2}$$ is 4. **Note:** In these types of problems, it is preferred to use a rotation matrix. This makes the problem much simpler for us to solve. We should remember that when rotating a point using a rotation matrix, the matrix containing the coordinates of the point comes after the rotation matrix in the product, that is $$\left[ {\begin{array}{*{20}{c}}a\\\b\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\dfrac{1}{2}}&{ - \dfrac{{\sqrt 3 }}{2}}\\\\{\dfrac{{\sqrt 3 }}{2}}&{\dfrac{1}{2}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}0\\\2\end{array}} \right]$$, and not $$\left[ {\begin{array}{*{20}{c}}a\\\b\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0\\\2\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\dfrac{1}{2}}&{ - \dfrac{{\sqrt 3 }}{2}}\\\\{\dfrac{{\sqrt 3 }}{2}}&{\dfrac{1}{2}}\end{array}} \right]$$. This is because a $$2 \times 1$$ matrix cannot be multiplied by a $$2 \times 2$$ matrix.