Question

Write down a unit vector in XY-plane, making an angle of ${{30}^{\circ }}$ with the
positive direction of x-axis.

Answer 1

Hint: If a unit vector is making an angle $\theta$ with the positive direction of x-axis, then it’s component along the x-axis is $\cos \theta$ and it’s component along the positive y-axis is $\sin\theta$. This unit vector will be written as $\cos \theta \widehat{i}+\sin \theta \widehat{j}$.

Before proceeding with the question, we must know the formula that will be required to solve this question. In vectors, if a unit vector is making an angle $\theta$ with the positive x-axis, then the vector can be written as $\cos \theta \widehat{i}+\sin \theta \widehat{j}$. The x component of this vector is $\cos \theta$ and the y component of this vector is $\sin \theta$.
In the question, we have to write down the unit vector making an angle ${{30}^{\circ }}$ with the positive x-axis.

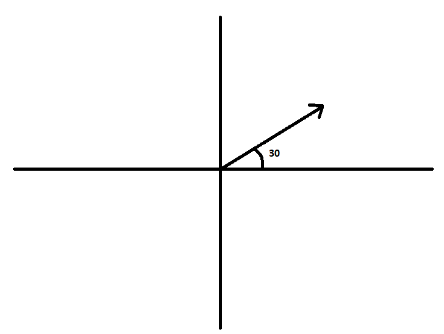
The x component of this vector will be $\cos {{30}^{\circ }}$ and the y component of this vector will be $\sin {{30}^{\circ }}$. So, this unit vector which is making an angle ${{30}^{\circ }}$ with the positive x-axis can be written as $\cos {{30}^{\circ }}\widehat{i}+\sin {{30}^{\circ }}\widehat{j}$.
From trigonometry, we have $\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}$ and $\sin {{30}^{\circ }}=\dfrac{1}{2}$. Substituting these values in the above vector, we get,
$\dfrac{\sqrt{3}}{2}\widehat{i}+\dfrac{1}{2}\widehat{j}$
There is one more possible vector that can make an angle of ${{30}^{\circ }}$ with the positive x-axis.
That vector is as shown below,

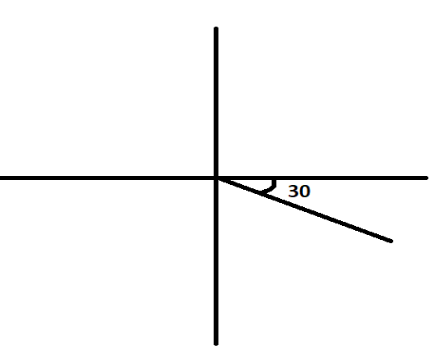
The x component of this vector will be $\cos {{30}^{\circ }}$ and the y component of this vector will be $\sin {{30}^{\circ }}$. But in this vector, the y component will be along the negative y-axis. So, this unit vector which is making an angle ${{30}^{\circ }}$ with the positive x-axis can be written as
$\cos {{30}^{\circ }}\widehat{i}-\sin {{30}^{\circ }}\widehat{j}$.
From trigonometry, we have $\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}$ and $\sin {{30}^{\circ }}=\dfrac{1}{2}$. Substituting these values in the above vector, we get,
$\dfrac{\sqrt{3}}{2}\widehat{i}-\dfrac{1}{2}\widehat{j}$
So, the two possible answers are $\dfrac{\sqrt{3}}{2}\widehat{i}+\dfrac{1}{2}\widehat{j}$ and $\dfrac{\sqrt{3}}{2}\widehat{i}-\dfrac{1}{2}\widehat{j}$.

Note: In this question, we were given a unit vector which is making an angle of ${{30}^{\circ }}$ with the positive x-axis. We wrote this vector by using the formula $\cos \theta \widehat{i}+\sin \theta \widehat{j}$. But in case we are given a vector which is also having a magnitude, let us say $r$and making an angle $\theta$ with the positive x-axis, we will write that vector by using the formula
$r\left( \cos \theta \widehat{i}+\sin \theta \widehat{j} \right)$.