Question

Write down a unit vector in the XY- plane, making an angle of 300 with the position direction of the x-axis.

Answer 1

A unit vector in the XY-plane indicates that there is no z-axis , we have to find the value of $\vec a = x\hat i + y\hat j$and for so that we will let a unit vector $\vec a$ and using the formula of dot product$\vec a.\vec b = \left| {\vec a} \right|\left| {\vec b} \right|\cos \theta$ we will find the value of x and y.

Complete step-by-step answer:
Step 1: Let the unit vector be$\vec a$, we know that $\vec a = x\hat i + y\hat j + z\hat k$, here the x-axis is $\hat i$, y-axis is $\hat j$ and z-axis is $\hat k$.
Since the vector is in XY-plane that means there is no z-coordinate (z=0)
Then, $\vec a = x\hat i + y\hat j + 0\hat k$
$\vec a = x\hat i + y\hat j$, the unit vector is in direction of x-axis is $\hat i$and y-axis is$\hat j$. According to the question $\vec a$ makes an angle of ${30^ \circ }$ with x-axis. So, the angle between $\vec a\& \hat i$is ${30^ \circ }$

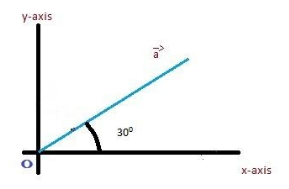
Step2: Now, using the formula of the dot product
$\vec a.\vec b = \left| {\vec a} \right|\left| {\vec b} \right|\cos \theta$ ( Is unit vector then its magnitude will be 1 i.e. $\left| {\vec a} \right|$=1), $\vec b = \hat i$ and $\theta = {30^ \circ }$
$\Rightarrow$ $\vec a.\hat i = \left| 1 \right|\left| {\hat i} \right|\cos {30^ \circ }$ (Similarly $\hat i$ is a unit vector, $\left| {\hat i} \right|$=1)
$\Rightarrow$ $\vec a.\hat i = 1.1.\dfrac{{\sqrt 3 }}{2}$ ($\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$)
$\Rightarrow$ $\vec a.\hat i = \dfrac{{\sqrt 3 }}{2}$ , and we have $\vec a = x\hat i + y\hat j + 0\hat k$, and $\hat i =$ $(1\hat i + 0\hat j + 0\hat k)$ putting this value we get,
$\Rightarrow (x\hat i + y\hat j + 0\hat k).\hat i = \dfrac{{\sqrt 3 }}{2} \\\ \Rightarrow (x\hat i + y\hat j + 0\hat k)(1\hat i + 0\hat j + 0\hat k) = \dfrac{{\sqrt 3 }}{2} \\\ \Rightarrow x.1 + y.0 + 0.0 = \dfrac{{\sqrt 3 }}{2} \\\ \Rightarrow x = \dfrac{{\sqrt 3 }}{2} \\\$
Step3: The angle between x and y-axis is${90^ \circ }$ and the angle between $\vec a\& \hat i$ is ${30^ \circ }$ so, the angle between is$\vec a\& \hat j = {60^ \circ }$. (As shown in the given figure)

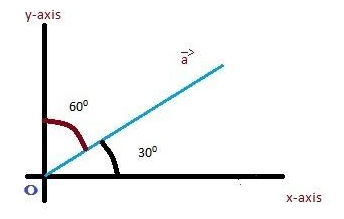
Similarly, using the same method
$\vec a.\vec b = \left| {\vec a} \right|\left| {\vec b} \right|\cos \theta$, substituting the value of $\vec b = \hat j\& \theta = {60^ \circ }$

\Rightarrow \vec a.\hat j = \left| {\vec a} \right|\left| {\hat j} \right|\cos 60 \\\ \Rightarrow \vec a.\hat j = 1.1\cos {60^ \circ } \\\ \Rightarrow \vec a.\hat j = \dfrac{1}{2} \\\ $$ ($$\cos {60^ \circ }$$=$$\dfrac{1}{2}$$) We have $\vec a = x\hat i + y\hat j + 0\hat k$ and $$\hat j = (0\hat i + 1\hat j + 0\hat k)$$

\Rightarrow (x\hat i + y\hat j + 0\hat k)(0\hat i + 1\hat j + 0\hat k) = \dfrac{1}{2} \\
\Rightarrow x.0 + y.1 + 0.0 = \dfrac{1}{2} \\
\Rightarrow y = \dfrac{1}{2} \\

$$STEP4: So now we have obtained both the value of x and y. Thus,$$

\Rightarrow \vec a = x\hat i + y\hat j \\
\Rightarrow \vec a = \dfrac{{\sqrt 3 }}{2}\hat i + \dfrac{1}{2}\hat j \\

**Note:** Always remember that a unit vector has a magnitude of 1. Don’t get confused while putting the value of $\theta $ because in step1 when we were finding the value of x then we have taken the angle between x and $\vec a$ i.e. ${30^ \circ }$ and when we were finding the value of y then we have taken the angle between y and $\vec a$ i.e. ${60^ \circ }$.