Question

Write Biot-Savart’s law for the magnetic field produced due to an element of a current carrying conductor and explain the term used in it. Define the unit of current with the help of it.

Answer 1

Use a current carrying conductor and derive the Biot-Savart’s law which shows the magnetic field produced due to a current carrying wire at a point outside the wire. The magnetic field is directly proportional to the current element and inversely proportional to distance between the point and the wire.

Complete step by step answer:
Biot and Savart presented a law for magnetic field produced due to an electric current element in the following form:
The intensity of magnetic due to an electric current element $Id\vec l$ at a point with position vector $\vec r$ with respect to electric current element is given by the formula as follows:
$d\vec B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Id\vec l \otimes \hat r}}{{{r^2}}}$
Here, $Id\vec l$ is the current element, that is the product of current and the line element of the conductor of very small length, ${\mu _0}$ is the magnetic permeability of vacuum whose value is $4\pi \times {10^{( - 7)}}\dfrac{{Tm}}{A}$ and $\hat r$is the unit vector, that is $\hat r = \dfrac{{\vec r}}{{{r^2}}}$ .

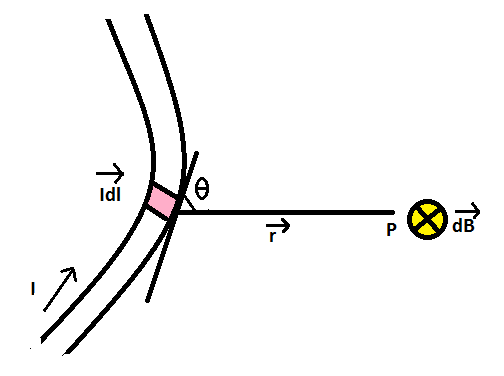
Let us consider a long wire carrying a current I and also consider a point p in the space. Let us also consider an infinitely small length of the wire dl at a distance r from the point P as shown. $\vec r$ is a distance-vector which makes an angle θ with the direction of current in the infinitesimal portion of the wire. The magnetic field density at point P due to that infinitesimal length dl of the wire is directly proportional to current carried by this portion of the wire.
As the current through that infinitesimal length of wire is the same as the current carried by the whole wire itself, we can write, because the current elements are continuous, the vector addition can be written as line integral in the following way:
$\vec{B}=\int{d\vec{B}=\dfrac{{{\mu }_{0}}}{4\pi }\int{1\centerdot \dfrac{d\vec{l}\times \hat{r}}{{{r}^{2}}}}}$
Above is the integral form of the Biot-Savart’s law.
The unit of current is ampere. Through Biot-Savart’s law, it can be defined as when 1 Tesla magnetic field is produced from a current carrying conductor at a distance of 1m; then 1 ampere current is produced.

Note:
It is important to derive the Biot-Savart’s law until its integral form. This law is similar to Coulomb’s law and Newton’s law of gravitation and can be easily applied to simple geometric objects. Biot-Savart’s law is also used to define magnetic field’s unit; When 1 ampere current is produced across a current carrying wire, then at a certain point 1 meter away from the wire, 1 Tesla magnetic field is produced.