Question
Question: Write any two necessary conditions for interference of light. Obtain an expression for fringe width ...
Write any two necessary conditions for interference of light. Obtain an expression for fringe width in Young's double slit experiment. Draw curve for intensity distribution in Young's double slit experiment.
Solution
Interference is the phenomenon in which two waves superimpose the lower, higher or same amplitude wave to form the resulting wave. Optical interference, or light interference, is the most commonly seen interference. Put the condition for the coherent light calculate θ and equate it from the condition of the coherent light for the dark width light put the condition of the dark fringe condition and equate it with the general equation of the fringe light.
Complete step by step solution:
Necessary conditions for interference of light
Light interference is a special phenomenon reflecting the nature of light as a wave. Two waves interfere with each other due to light interference and where crest and crest or trough and trough meet the light amplitude becomes very large and constructive interference occurs, we say.
Interference happens when two waves of the same frequency are present at the same location simultaneously and are coherent. The two waves combine to form a single wave, the intensity of which depends not only on the intensity of the two waves, but also on the difference in phases between them.
2)Light should be coherent lights. =ΔS1 S2M
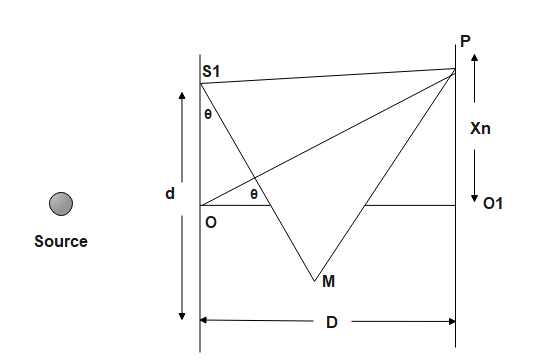
=sinθ=dS2M
=θ=dS2M
=ΔOO1P
=tanθ=DXn
=θ=DXn
=dS2M=DXn
=S2M=DXn⋅d
=DXn=nλ
=Xn=dn2D
For dark fringe width (βdark )
=βdark =Xn+1−Xn
=Xn+1−Xn
=(n+1)dλD−dnλD
=dλD(n+1−n)
=βdark =dλD
=For bright fringe width (βBright ): =DXnd=(2n+1)2λ
=βBright =Xn+1−Xn
=βBright =(2(n+1)+1)2 dλD−(2n+1)2 dλD
=2 dλD(2n+2+1−2n−1)
=2 dλD⋅2
=βBright =dλD
=βBright =dλD is the expression for fringe width in Young's double slit experiment.
The curve for intensity distribution in Young's double slit experiment.
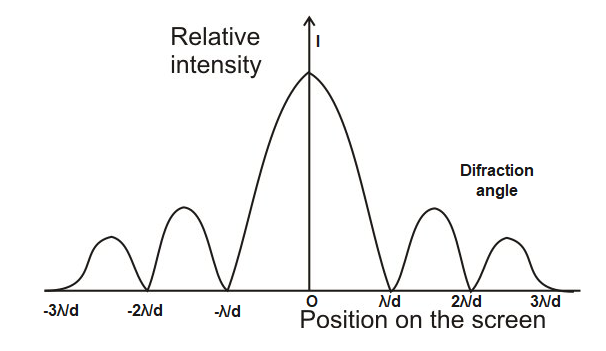
Note:
They will interfere with each other when the waves reflected from the inner and outer surface combine, removing or reinforcing some parts of white light through destructive or constructive interference. Consider a pair of light waves that are travelling, for example, in direction D, from the same source. Two types of interference are different: proactive interference and retroactive interference.
