Question

Write Ampere’s circuital law. Obtain an expression for the magnetic field on the axis of current carrying a very long solenoid. Draw necessary diagrams.

Answer 1

Hint : To solve this question, we have to consider a square boundary partially inside the long solenoid. Then applying ampere’s circuital law on all of its four sides will give the final expression for the magnetic field on its axis.

Complete step by step answer:
The Ampere’s circuital law states that the line integral of the magnetic field along a boundary enclosing a surface is equal to ${\mu _0}$ times the total current passing normal to the surface, that is,
$\oint {B \cdot dl} = {\mu _0}{I_T}$ (1)
Consider a part of solenoid of infinite length, having $n$ turns per unit length, in which $I$ current is flowing, as shown in the below diagram.

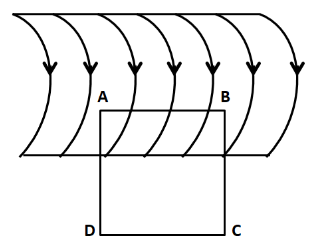
Here we have considered a square ABCD lying partially inside the region of the solenoid. Let the side of the square ABCD be $l$ . Now, from the LHS of the Ampere’s circuital law we get
$\oint {B \cdot dl} = \oint {{B_{AB}} \cdot dl} + \oint {{B_{BC}} \cdot dl} + \oint {{B_{CD}} \cdot dl} + \oint {{B_{DA}} \cdot dl}$ (2)
As the sides BC and CD are perpendicular to the magnetic field of the solenoid, so both the terms $\oint {{B_{BC}} \cdot dl}$ and $\oint {{B_{CD}} \cdot dl}$ are equal to zero.
Also, as the side DC is lying outside the solenoid, so no magnetic field will lie along it. Therefore ${B_{DA}} = 0$ which gives $\oint {{B_{DA}} \cdot dl}$ equal to zero.
Therefore (2) reduces to
$\oint {B \cdot dl} = \oint {{B_{AB}} \cdot dl}$
As the solenoid is infinite, so the field will be uniform, and so we can have
$\oint {B \cdot dl} = B\oint {dl}$ $\left( {{B_{AB}} = B} \right)$
As the side of square is equal to $l$ , so we have
$\oint {B \cdot dl} = Bl$ (3)
Now, the total current flowing normal to the side AB is
${I_T} = I\left( {nl} \right)$
So the RHS of the Ampere’s circuital law becomes
${\mu _0}{I_T} = {\mu _0}I\left( {nl} \right)$ (4)
Putting (3) and (4) in (1)
$Bl = {\mu _0}I\left( {nl} \right)$
Cancelling $l$ from both the sides, we get
$B = {\mu _0}nI$
Hence, the magnetic field of the axis of current carrying a very long solenoid is equal to ${\mu _0}nI$ .

Note:
While deriving the magnetic field on the axis of a solenoid, the boundary chosen must be of square or rectangular shape only, Other shapes, like circle or ellipse should be chosen as they will make the calculations very much complex.