Question

Write Ampere circuital law in mathematical form. Derive an expression of magnetic field the axis of current carrying long solenoid. Draw necessary diagrams.

Answer 1

Ampere's circuital law relates the closed loop's magnetic field to the loop's current and circumference. The integral of the magnetic field along a closed loop is equal to the product of current in the loop and permeability of the free space. The magnetic field's intensity is the same as the number of magnetic field lines at a point inside the solenoid.

Complete step-by-step solution :
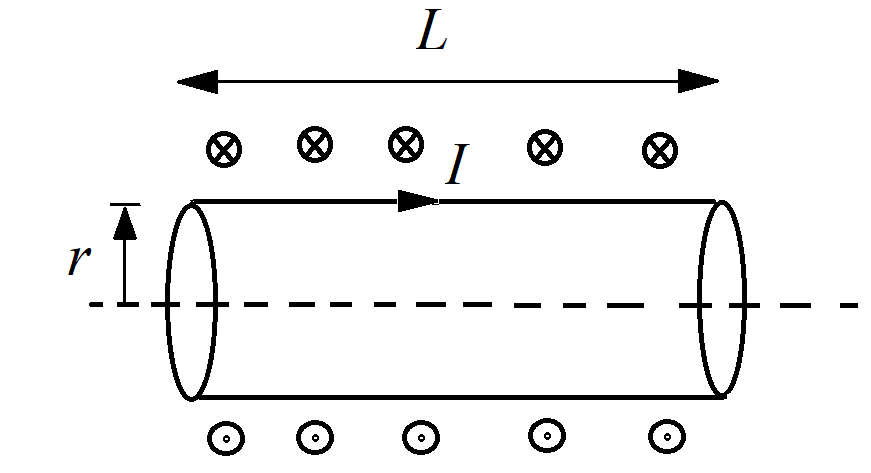
Let the electric current through the loop is $I$ and length of the loop is L.
Write the mathematical expression of Ampere law.
$\oint {B \cdot dl} = {\mu _0}I$
Here, ${\mu _0}$ is the permeability of the free space, B is the magnetic field of the solenoid and $I$ is the current in the solenoid.

The shape of the solenoid is like a cylinder, so the line integral along the solenoid is the same as the circumference of the solenoid. The value of the circumference of the solenoid is $2\pi r$.

The diagram of the current carrying long solenoid is shown below:

Substitute the known values in the above expression.
$B\int {dl} = {\mu _0}I$
$B\left( {2\pi r} \right) = {\mu _0}I$
$B = \dfrac{{{\mu _0}I}}{{2\pi r}}$
Here, r is the radius of the solenoid.

The solenoid's magnetic field depends on the current in the solenoid and distance from the axis of the solenoid. The current direction may vary in the solenoid; it may be either inside the paper or outside the paper according to the clockwise or anticlockwise direction of the current in the solenoid.

Thus, the magnetic field of the axis of current carrying a long solenoid is $\dfrac{{{\mu _0}I}}{{2\pi r}}$.

Note:- Be sure in the calculation of the total length of the loop because only that length of the loop is considered, which encloses the loop. The direction of the current decides the direction of the magnetic field, so the direction of the current must be mentioned in the diagram.