Question

Write all the unit vectors in XY- plane.

Answer 1

For solving this question you should know about the unit vectors in planes. A unit vector in the XY- plane indicates that there is no Z-axis, we have to find the value of $\overrightarrow{a}=x\widehat{i}+y\widehat{j}$ and for that we will let a unit vector $\overrightarrow{a}$ and using the formula of dot product $\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta$ we will find the value of X and Y.

Complete step-by-step solution:
According to our question it is asked to write all the unit vectors in the XY- plane. Let the unit vector be $\overrightarrow{a}$, we know that $\overrightarrow{a}=x\widehat{i}+y\widehat{j}+z\widehat{k}$, where x-axis is $\widehat{i}$, y-axis is $\widehat{j}$ and z-axis is$\widehat{k}$. Since the vector is in XY-plane, that means there is no z-coordinate (z = 0). Then,
$\begin{aligned} & \overrightarrow{a}=x\widehat{i}+y\widehat{j}+0\widehat{k} \\\ & \Rightarrow \overrightarrow{a}=x\widehat{i}+y\widehat{j} \\\ \end{aligned}$
The unit vector in the direction of x-axis is $\widehat{i}$ and y-axis is $\widehat{j}$.

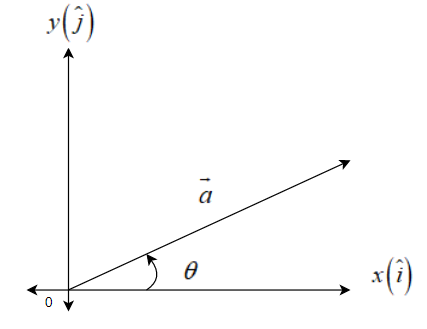
Angle with x-axis:
Since $\overrightarrow{a}$ makes an angle of $\theta$ with x-axis, so angle between $\overrightarrow{a}$ and $\widehat{i}$ is $\theta$.
We know that: $\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta$
So, putting $\overrightarrow{a}=\overrightarrow{a,}\overrightarrow{b}=\widehat{i,}\theta =\theta$
$\overrightarrow{a}.\widehat{i}=\left| \overrightarrow{a} \right|\left| \widehat{i} \right|\cos \theta$
As $\overrightarrow{a}$ is a unit vector, $\left| \overrightarrow{a} \right|=1$ and $\widehat{i}$ is a unit vector, $\left| \widehat{i} \right|=1$. So,
$\begin{aligned} & \overrightarrow{a}.\widehat{i}=1\times 1\times \cos \theta \\\ &\Rightarrow \overrightarrow{a}.\widehat{i}=\cos \theta \\\ &\Rightarrow \left( x\widehat{i}+y\widehat{j}+0\widehat{k} \right).\widehat{i}=\cos \theta \\\ &\Rightarrow \left( x\widehat{i}+y\widehat{j}+0\widehat{k} \right).\left( 1\widehat{i}+0\widehat{j}+0\widehat{k} \right)=\cos \theta \\\ &\Rightarrow x.1+y.0+0.0=\cos \theta \\\ &\Rightarrow x=\cos \theta \\\ \end{aligned}$

Angle with y-axis:
Since $\overrightarrow{a}$ makes an angle of $\left( {{90}^{\circ }}-\theta \right)$ with y-axis, so angle between $\overrightarrow{a}$ and $\widehat{j}$ is $\left( {{90}^{\circ }}-\theta \right)$.
We know that: $\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta$
So, putting $\overrightarrow{a}=\overrightarrow{a,}\overrightarrow{b}=\widehat{j,}\theta =\left( {{90}^{\circ }}-\theta \right)$
$\begin{aligned} & \overrightarrow{a}.\widehat{j}=\left| \overrightarrow{a} \right|\left| \widehat{j} \right|\cos \left( {{90}^{\circ }}-\theta \right) \\\ &\Rightarrow \overrightarrow{a}.\widehat{j}=1\times 1\times \cos \left( {{90}^{\circ }}-\theta \right) \\\ &\Rightarrow \overrightarrow{a}.\widehat{j}=\cos \left( {{90}^{\circ }}-\theta \right) \\\ &\Rightarrow \overrightarrow{a}.\widehat{j}=\sin \theta \\\ &\Rightarrow \left( x\widehat{i}+y\widehat{j}+0\widehat{k} \right).\widehat{j}=\sin \theta \\\ &\Rightarrow \left( x\widehat{i}+y\widehat{j}+0\widehat{k} \right).\left( 0\widehat{i}+1\widehat{j}+0\widehat{k} \right)=\sin \theta \\\ &\Rightarrow x.0+y.1+0.0=\sin \theta \\\ &\Rightarrow y=\sin \theta \\\ \end{aligned}$
Thus,
$\begin{aligned} & \overrightarrow{a}=x\widehat{i}+y\widehat{j} \\\ &\Rightarrow \overrightarrow{a}=\cos \theta \widehat{i}+\sin \theta \widehat{j} \\\ \end{aligned}$
This value will be true in all quadrants. So, $0\le \theta \le 2\pi$.
Therefore $\overrightarrow{a}=\cos \theta \widehat{i}+\sin \theta \widehat{j}$; for $0\le \theta \le 2\pi$.

Note: While solving this type of questions you should be careful of the angles from the x-axis and y-axis and always, we have to make a unit vector. And this will be mandatory to be in the XY-plane. And if it is in the XY-plane, then the rest Z-plane coordinate must be always zero.