Question

Write a unit vector in the direction of the sum of the vectors $=2\hat{i}+2\hat{j}-5\hat{k}$ and $=2\hat{i}+\hat{j}-7\hat{k}$.

Answer 1

In this question, in order find a unit vector in the direction of the sum of the vectors $=2\hat{i}+2\hat{j}-5\hat{k}$ and $=2\hat{i}+\hat{j}-7\hat{k}$ we will first evaluate the sum of the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$. Then we know that for a vector $=x\hat{i}+y\hat{j}+z\hat{k}$, the magnitude of the vector $=x\hat{i}+y\hat{j}+z\hat{k}$ is denoted by $\left| \right|$ is given by $\left| \right|=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$ . Also the unit vector of the vector $$$$ is given by $\dfrac{}{\left| \right|}$ which is equals $\dfrac{}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}$. Now using this we will have to find the magnitude of the vector $\overrightarrow{a}+\overrightarrow{b}$ which is denoted by $\left| \overrightarrow{a}+\overrightarrow{b} \right|$ and then in order to evaluate the unit vector of the sum $\overrightarrow{a}+\overrightarrow{b}$, we will have to find $\dfrac{\overrightarrow{a}+\overrightarrow{b}}{\left| \overrightarrow{a}+\overrightarrow{b} \right|}$.

Complete step by step answer:
Let the vector $\overrightarrow{a}$ is given by $=2\hat{i}+2\hat{j}-5\hat{k}$ and the vector $\overrightarrow{b}$ is given by $=2\hat{i}+\hat{j}-7\hat{k}$.
On plotting this points on the graph we have

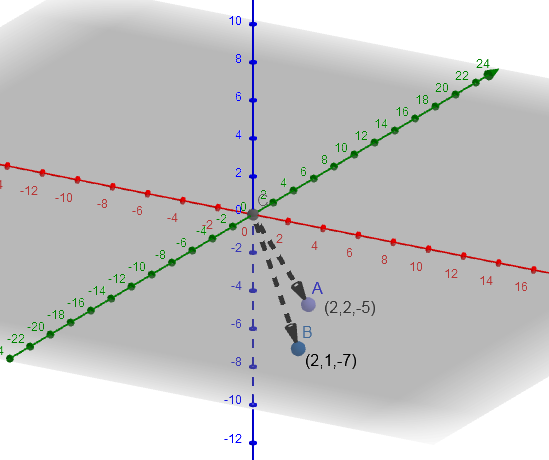
Now the sum of both the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ is given by the sum $\overrightarrow{a}+\overrightarrow{b}$.
That is

& \overrightarrow{a}+\overrightarrow{b}=\left( 2\hat{i}+2\hat{j}-5\hat{k} \right)+\left( 2\hat{i}+\hat{j}-7\hat{k} \right) \\\ & =\left( 2+2 \right)\hat{i}+\left( 2+1 \right)\hat{j}+\left( -5-7 \right)\hat{k} \\\ & =4\hat{i}+3\hat{j}-12\hat{k} \\\ \end{aligned}$$ Therefore we have $$\overrightarrow{a}+\overrightarrow{b}=4\hat{i}+3\hat{j}-12\hat{k}.............(1)$$. Now since we know that for a vector $$=x\hat{i}+y\hat{j}+z\hat{k}$$, the magnitude of the vector $$=x\hat{i}+y\hat{j}+z\hat{k}$$ is denoted by $$\left| \right|$$ is given by $$\left| \right|=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$$ . Thus magnitude of the vector $$\overrightarrow{a}+\overrightarrow{b}$$ which is denoted by $$\left| \overrightarrow{a}+\overrightarrow{b} \right|$$. Now comparing the sum $$\overrightarrow{a}+\overrightarrow{b}$$ with the vector $$=x\hat{i}+y\hat{j}+z\hat{k}$$, we will get $$x=4,y=3$$ and $$z=-12$$. Thus on calculating the magnitude of the sum $$\overrightarrow{a}+\overrightarrow{b}$$, we will have $$\begin{aligned} & \left| \overrightarrow{a}+\overrightarrow{b} \right|=\sqrt{{{4}^{2}}+{{3}^{2}}+{{\left( -12 \right)}^{2}}} \\\ & =\sqrt{16+9+144} \\\ & =\sqrt{169} \end{aligned}$$ Now we know that $$\sqrt{169}=\pm 13$$, but the magnitude of the vector cannot be negative. Therefore we have $$\begin{aligned} & \left| \overrightarrow{a}+\overrightarrow{b} \right|=\sqrt{169} \\\ & =13...............(2) \end{aligned}$$ Also since we know that the unit vector of the vector $$$$ is given by $$\dfrac{}{\left| \right|}$$ which is equals $$\dfrac{xi+yj+zk}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}$$. In order to calculate the unit vector of the sum $$\overrightarrow{a}+\overrightarrow{b}$$, we will have to find $$\dfrac{\overrightarrow{a}+\overrightarrow{b}}{\left| \overrightarrow{a}+\overrightarrow{b} \right|}$$. Now we will substitute the values in equation (1) and equation (2) in $$\dfrac{\overrightarrow{a}+\overrightarrow{b}}{\left| \overrightarrow{a}+\overrightarrow{b} \right|}$$, we will get $$\begin{aligned} & \dfrac{\overrightarrow{a}+\overrightarrow{b}}{\left| \overrightarrow{a}+\overrightarrow{b} \right|}=\dfrac{4\hat{i}+3\hat{j}-12\hat{k}}{13} \\\ & =\dfrac{4}{13}\hat{i}+\dfrac{3}{13}\hat{j}-\dfrac{12}{13}\hat{k} \end{aligned}$$. Therefore the unit vector in the direction of the sum of the vectors $$=2\hat{i}+2\hat{j}-5\hat{k}$$ and $$=2\hat{i}+\hat{j}-7\hat{k}$$ is given by $$\dfrac{4}{13}\hat{i}+\dfrac{3}{13}\hat{j}-\dfrac{12}{13}\hat{k}$$. **Note:** In this problem, please to don consider the magnitude of the vector $$\overrightarrow{a}+\overrightarrow{b}$$ as $$-13$$ and then substitute in into $$\dfrac{\overrightarrow{a}+\overrightarrow{b}}{\left| \overrightarrow{a}+\overrightarrow{b} \right|}$$ to find the unit vector of the sum because the magnitude of the vector cannot be negative.