Question

Write a short note in the simple harmonic of the pendulum.

Answer 1

The force is acting on the mass. Split the force due to gravity into two perpendicular components Equate the restoring force of the mass to the $x$ component of the force and the acceleration is directly proportional to the displacement of the mass from the mean position.
Formula used:
$T = mg{\text{ }}cos\left( c \right)$
$F{\text{ }} = {\text{ }} - mg{\text{ }}sin\left( c \right)$
$F = ma$

Complete step-by-step solution:

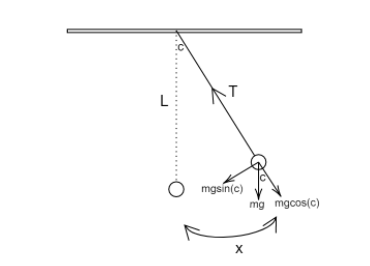
Let us consider a simple pendulum with a mass, $m$ swinging by a massless string. Let the string be displaced by a small angle $c$. Let the length of the simple pendulum be $L$. Let $T$ be the tension on the string. Let us consider the case where the angle made by the string to the normal is $c$. Force due to gravity can be split into two perpendicular components: ${G_x}$ and ${G_y}$ where,

{{G_x}{\text{ }} = mgsin\left( c \right)} \\\ {{G_y} = mg{\text{ }}cos\left( c \right)} \end{array}$$ The tension on the string is balanced by the $y$ component of force due to gravity. So, $$T = mg{\text{ }}cos\left( c \right)$$ And$x$ a component of force due to gravity acts as the restoring force. So, $$F{\text{ }} = {\text{ }} - mg{\text{ }}sin\left( c \right)$$ Since the angle made is very small, we can do an approximation as follows. $$sin\left( c \right) \approx c$$ The angle can be written as arc length divided by the radius of a circle. Using this relation in the given diagram, we get $c = \dfrac{l}{x}$ Therefore, substituting this value of angle into the equation of restoring force, we get $$F = - mg\dfrac{1}{x}$$ According to Newton's second law, $F = ma$ Equating the above equations for the force, we get $ma = - mg\dfrac{x}{l}$ Canceling the common term of mass on both sides, we get an equation for acceleration as follows, $a = - \dfrac{g}{l}x$ $ \Rightarrow a\alpha - x$ And this is precisely the condition for a simple harmonic oscillator; that is, acceleration is directly proportional to the displacement from the mean position. Thus, the oscillation of a simple pendulum is an example of a simple harmonic oscillator **Note:** We have made two approximations in the above proof. We have assumed the string to be massless and we have assumed the angle displaced to be very small for our convenience. It doesn't necessarily work for other cases.