Question

Write a description of each shaded area. Use the symbols $U,A,B, \cup , \cap$ and $\backslash$ as necessary.

Answer 1

We use the definition universal sets and the given sets in the Venn diagram. Use definitions of Union, intersection and subtraction of sets to write the solution for each part.

• Venn diagram is a diagram that represents sets pictorially in the form of circles. All sets are contained inside a rectangular region which represents the universal set.

Complete step-by-step answer:
We first write the definitions of each term given in the question.
Universal set (U): Universal set is a set that contains all sets inside it.
Union of sets ($\cup$): Union of two or more sets denotes the set that contains elements that are in either set or both sets.
Intersection of sets ($\cap$): Intersection of two or more sets denotes the set that contains the common elements of both the sets.
Subtraction of sets ($\backslash$): Subtraction of a set from another set denotes the elements that are in one set but not in another set.
Now we solve each part separately.
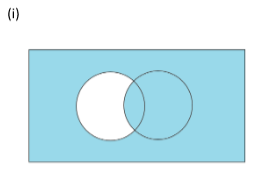
(i) We write the two sets given in the form of circles as ‘A’ and ‘B’ and the rectangle as ‘U’. Then the diagram becomes

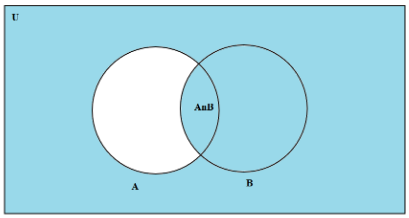
We have to write a description of the shaded area.
Here the shaded area includes the whole set ‘B’, complete universal set ‘U’ and excludes the area of set ‘A’ only.
Shaded region is $U\backslash \left( {A\backslash (A \cap B)} \right)$
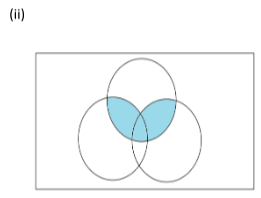
(ii) We write the three sets given in the form of circles as ‘A’, ‘B’ and ‘C’ and the rectangle as ‘U’. Then the diagram becomes

Here the shaded area includes the intersection of sets ‘A’ with ‘B’ and intersection of the sets ‘A’ with ‘C’.
Shaded region is $\left( {A \cap B} \right) \cup \left( {A \cap C} \right)$
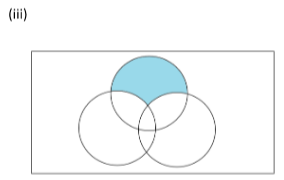
(iii) We write the three sets given in the form of circles as ‘A’, ‘B’ and ‘C’ and the rectangle as ‘U’. Then the diagram becomes

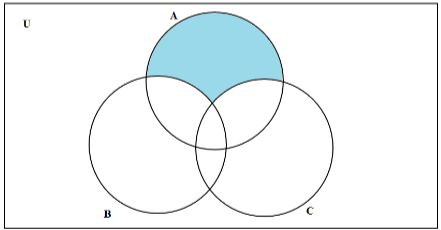
Here the shaded area includes the set ‘A’ only. So we can say the shaded area has set ‘A’ minus the intersection of ‘A’ with ‘B’, minus the intersection ‘A’ with ‘C’ plus intersection of sets ‘A’, ‘B’ and ‘C’.
Shaded region is A\backslash \left\\{ {\left( {(A \cap B) \cup (A \cap C)} \right)\backslash \left( {A\cap B \cap C} \right)} \right\\}
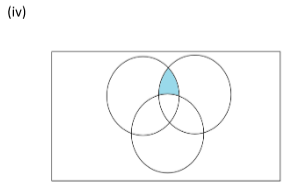
(iv) We write the three sets given in the form of circles as ‘A’, ‘B’ and ‘C’ and the rectangle as ‘U’. Then the diagram becomes

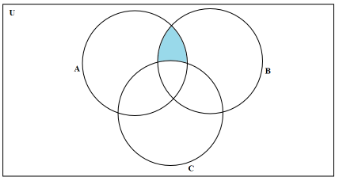
Here the shaded area includes the intersection of sets ‘A’ and ‘B’ minus the intersection of ‘A’, ‘B’ and ‘C’.
Shaded region is $\left( {A \cap B} \right)\backslash \left( {A \cap B \cap C} \right)$

Note: Students are advised to use the necessary symbols only, otherwise there are many ways to depict the above given shaded regions. Many students make mistakes in writing the description of the shaded region as they get confused with union and intersection, intersection represents the word ‘and’ whereas union represents the words ‘either, or’. Keep in mind it is always easy if we shade the regions step by step and then write the final answer.