Question

Work is said to be done if the force and displacement are
A. parallel to each other
B. opposite to each other
C. inclined at an angle with each other $\theta \left( \ne {{90}^{\circ }} \right)$
D. all of the above

Answer 1

Hint: Work is said to be the measurement of energy used in moving an object, mostly it is force times displacement. If an object is at rest or does not move, the work done is considered to be zero.

Complete step by step answer:
When a force is applied on an object for a particular distance, it is considered that a work is done on that object. Work done is the change in kinetic energy of the object. The SI unit of work is newton-meter or joule.
$N\times m=kg\dfrac { { m }^{ 2 } }{ { s }^{ 2 } } =J$
Work done on an object along a particular direction of motion is given as force times displacement times the cosine of the angle, which can be written as
$W=F\times d\times \cos { \theta }$
Where, ‘F’ is the force applied and ‘d’ is the displacement of the object.

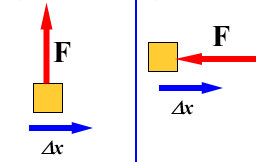
Let us consider the first case where the force and displacement are parallel to each other, which means $\theta =0$. Then work done becomes,
$W=F\times d$, that means the work is said to be done.
For the second case where the force and displacement are opposite to each other, $\theta =180$. Then work done becomes,
$W=-F\times d$, this also means the work is said to be done.
In the third case where the force and displacement are inclined at an angle θ with each other, the work done becomes
$W=F\times d\times \cos { \theta }$
The work is said to be done in all the three cases.
Therefore, the correct answer for the given question is option (D).

Note: No work is said to be done, if the direction of motion of force is perpendicular, which means $\theta ={{90}^{\circ }}$ and $\cos {{90}^{\circ }}=0$ therefore work done becomes zero. On considering force acting parallel to the direction of motion, we neglect the cosine term as it does not change the expression.