Question
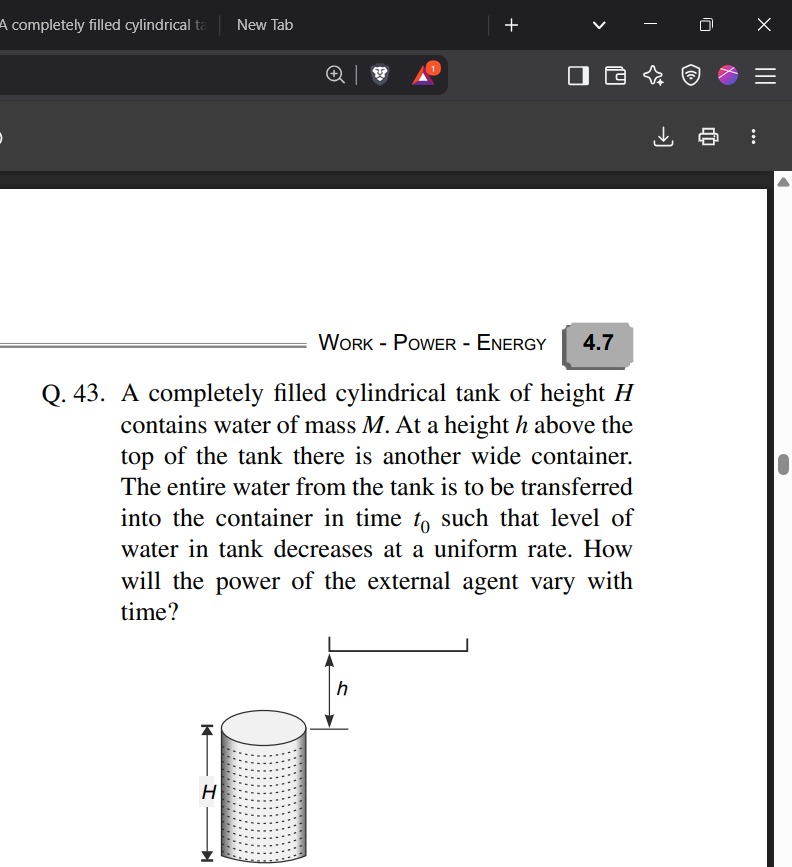
Question: A completely filled cylindrical tank of height $H$ contains water of mass $M$. At a height $h$ above...
A completely filled cylindrical tank of height H contains water of mass M. At a height h above the top of the tank there is another wide container. The entire water from the tank is to be transferred into the container in time t0 such that level of water in tank decreases at a uniform rate. How will the power of the external agent vary with time?
P(t) = \frac{M g}{t_0} \left(h + \frac{H}{t_0}t\right)
Solution
The power required to transfer water is the product of the mass flow rate, gravitational acceleration, and the instantaneous height the water is lifted. The mass flow rate is constant because the water level decreases at a uniform rate. The instantaneous height the water is lifted increases linearly with time because as water is drained, it is lifted from progressively lower depths in the tank to the fixed height of the receiving container. Combining these, the power varies linearly with time.
