Question
Question: Without using distance formula, show that points (-2, -1), (4, 0), (3,3) and (-3, 2) are the vertice...
Without using distance formula, show that points (-2, -1), (4, 0), (3,3) and (-3, 2) are the vertices of a parallelogram.
Solution
Hint: We know that in a parallelogram, the diagonals bisect each other. So, we may find here the mid points of both the diagonals using the given four points and if the midpoint comes out the same then it will be proved that the given points form a parallelogram.
Complete Step-by-step answer:
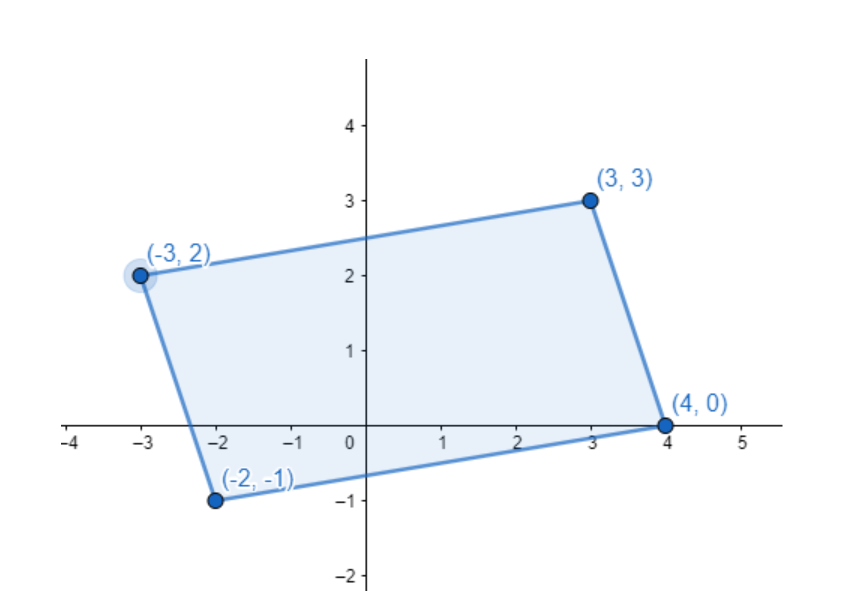
For finding the mid-points of the diagonal we may use here the midpoint formula. So, according to the midpoint formula: -
If we are given with two points, say (a, b) and (x, y) then the mid-point of the line joining these two points is given as:
(2a+x,2b+y)
We will use this formula for finding the mid-points of the diagonals.
First we consider the diagonal formed by the points (-3,2) and (4,0).
The mid-point of the line joining these two points will be:
(2−2+3,2−1+3)=(2−1,1)
Now we should consider the diagonal formed by the points (-2,-1) and (3,3).
The mid-point of the line joining these two points is:
(2−2+3,2−1+3)=(2−1,1)
So, we can see that the mid-points of both the diagonals are the same. It means that diagonals are bisecting each other.
Hence, the given four points are the vertices of a parallelogram.
Note: Students should note here that the diagonals of a parallelogram bisect each other and hence the mid-points of both diagonals are the same. Here the chance of mistake is that instead of taking the coordinates of diagonals students can make mistakes by taking the coordinates of sides of the parallelogram. So, the coordinates should be taken properly.
