Question

Within a spherical charge distribution of charge density $\rho$ (r), N equipotential surfaces of potential ${V_O}$ +$V + \Delta {V_O}$, ${V_O} + 2\Delta V$,…..,${V_O} + N\Delta V$($\Delta V$>0), are drawn and have increasing radii ${r_o}$,${r_1}$,${r_2}$,…..${r_N}$ respectively. If the difference in the radii of the surfaces is constant for all values of ${V_O}$ and $\Delta V$ then:
A) $\rho$ (r)=constant
B) $\rho$ (r)$\alpha$ $\dfrac{1}{{{r^2}}}$
C) $\rho$ (r)$\alpha$ $\dfrac{1}{r}$
D) $\rho$ (r)$\alpha$1

Answer 1

The question is simple as it is based on the Gaussian law and its charged surface. According to the question it has N equipotential surfaces with increasing radii, so we will take out a small element dr from the sphere, apply Gaussian law on it and integrate it from limit 0 to radius r and then find the proportionality of density. Formula used = $\int {\mathop E\limits^ \to \cdot \mathop {ds}\limits^ \to }$ = $\dfrac{{\left( {{q_{enclosed}}} \right)}}{{{E_o}}}$ q(enclosed) is the charge distributed in area. Use the area of the sphere as $\dfrac{4}{3}\pi {r^3}$.

Complete step by step solution:
Step 1:
The Gaussian surface is known as a closed surface in three-dimensional space such that the flux of a vector field is calculated. These vector fields can either be the gravitational field or the electric field or the magnetic field. Using Gauss law, Gaussian surface can be calculated:
Gaussian surface of sphere is represent as $\int {\mathop E\limits^ \to \cdot \mathop {ds}\limits^ \to }$ =$\dfrac{{\left( {{q_{enclosed}}} \right)}}{{{E_o}}}$ q(enclosed) is the charge distributed in area.
In any two successive equipotential surfaces have potential difference equal to $\Delta V$
We have to find how the value of $\rho$ (r) depend of r
Spherical charge distribution is given with charge density $\rho$ (r)

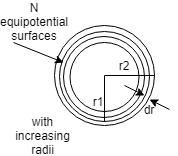
The spherical shell is there of thickness dr which is very small and having inner radius $r_1$ and outer radius $r_2$. To find the whole charge distribution we will find charge in a small element and then integrate for the whole sphere.

Step 2:
Applying Gaussian law on the Gaussian surface$\int {\mathop E\limits^ \to \cdot \mathop {ds}\limits^ \to }$ =$\dfrac{{{q_{enclosed}}}}{{{E_o}}}$
(q(enclosed) is the charge distributed in area)
Then, $\int {\mathop E\limits^ \to \cdot } \mathop {ds}\limits^ \to = \dfrac{{\left( {{q_{enclosed}}} \right)}}{{{E_0}}} \Rightarrow \int\limits_0^r {\dfrac{{\rho \left( r \right)\left( {4\pi {r^2}} \right)dr}}{{{E_0}}}}$
(integrating from 0 to r to find whole electric field)
The equipotential surfaces of potential ${V_O}$ +$V + \Delta {V_O}$, ${V_O} + 2\Delta V$,…..,${V_O} + N\Delta V$($\Delta V$>0) and increasing radii${r_o}$,${r_1}$,${r_2}$,…..${r_N}$ Are in a form of A.P and hence are constant with respect to each other
Or we can say that E= −$\dfrac{{\Delta V}}{{\Delta r}}$ (constant)
Now, $\int\limits_{area} {E \cdot dA} = \dfrac{{{q_{enclosed}}}}{{{E_o}}} \Rightarrow \int\limits_{area} {E \cdot dA} = \int\limits_0^r {\dfrac{{\rho \left( r \right)4\pi {r^2}dr}}{{{E_o}}}}$ ……. (1)
Here, dA is the area of Gaussian
Surface and Gaussian surface is sphere so area A is equal to $4\pi {r^2}$.
Rewriting equation (1), $E\left( {4\pi {r^2}} \right) = \int\limits_0^r {\dfrac{{\rho \left( r \right)\left( {4\pi {r^2}} \right)dr}}{{{E_0}}}}$ …….. (2)
(Cancelling $4\pi {r^2}$ both sides)
$\Rightarrow$ $\left( {E{E_o}} \right){r^2} = \int\limits_0^r {\rho \left( r \right){r^2}dr}$
If we will say $E{E_o}$ is constant.
From here we understood that $\int\limits_0^r {\rho \left( r \right)\left( {{r^2}} \right)dr}$ $\alpha$ ${r^2}$ in integration power increase by one. If this equation is true then $\rho$ (r)$\propto$ $\dfrac{1}{r}$ must be true.
Say, $\rho \left( r \right)$ =$\dfrac{C}{r}$ putting in (2) $\int\limits_0^r {\dfrac{C}{r} \cdot {r^2}dr = k \cdot {r^2}}$ where k is some proportionality constant.
Solving the left hand side, $\dfrac{C}{2}{r^2}$ and it is proportional. So we can say that $\rho \left( r \right)\propto \dfrac{1}{r}$.

Hence option (C) is correct.

Note: Points to remember:
While solving the equation for the Gaussian surface must read which object is given. At the place of area we need to write the area of that object, for example we are given a spherical shell so we have used the area of the sphere. Also we have taken a small element dr and integrated it to find the whole of E. At the end we have made LHS=RHS to find the relation of charge density with r.