Question: With what minimum acceleration can a fireman slide down a rope while breaking strength of the rope i...

Question

With what minimum acceleration can a fireman slide down a rope while breaking strength of the rope is $\dfrac{2}{3}$ of the weight?
(A). $\dfrac{2}{3}g$
(B). $g$
(B). $\dfrac{1}{3}g$
(D). Zero

Answer 1

Solution

These types of questions can be easily solved using Newtonian physics. Firstly understand the problem thoroughly, and then draw a simple diagram dissipating the same for better understanding. Lastly apply Newton’s law of motion to find the required answer.

Formula Used :
$ma = mg - T$
where T is the tension in the string,
a is the downwards acceleration,
g is the acceleration due to gravity,
and m is the mass of the fireman.

Complete step-by-step answer :
Given: There is a rope whose breaking strength is $\dfrac{2}{3}$ the weight of a fireman. And we are asked to calculate the minimum acceleration with which the fireman can slide down this rope.
The following diagram dissipates the given problem perfectly:

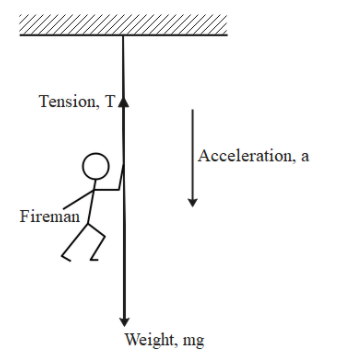
Let the weight of the fireman be mg and his downward acceleration be a.
Breaking strength of rope, $T = \dfrac{2}{3}mg{\text{ }}\left( {given} \right)$
Using Newton’s second law of motion which states that the acceleration of a particle as measured from an inertial frames given by the vector sum of all the forces acting on the particle divided by its mass, we have:
$\eqalign{ & ma = mg - T \cr & \Rightarrow ma = mg - \dfrac{2}{3}mg \cr & \Rightarrow ma = \dfrac{1}{3}mg \cr & \Rightarrow a = \dfrac{g}{3} \cr}$
Therefore, the minimum acceleration by which a fireman can slide down a rope while breaking strength of the rope is $\dfrac{2}{3}$ of the weight is $\dfrac{1}{3}g$ .
So, the correct answer for the given question is C. i.e., $\dfrac{1}{3}g$ .

Note :
Students often get the answer wrong for these types of questions because they fail to draw a proper diagram and then apply Newton's law. It is very crucial to draw the diagram; otherwise students can make errors in assuming the direction vectors of the forces resulting in wrong and meaningless equations. Which in turn would obviously result in wrong answers.