Question
Question: With usual notations, in $\triangle ABC$ if a = 2, b = 3, c = 5 and $\frac{cos A}{a}+\frac{cos B}{b}...
With usual notations, in △ABC if a = 2, b = 3, c = 5 and acosA+bcosB+ccosC=30k+7 then k =
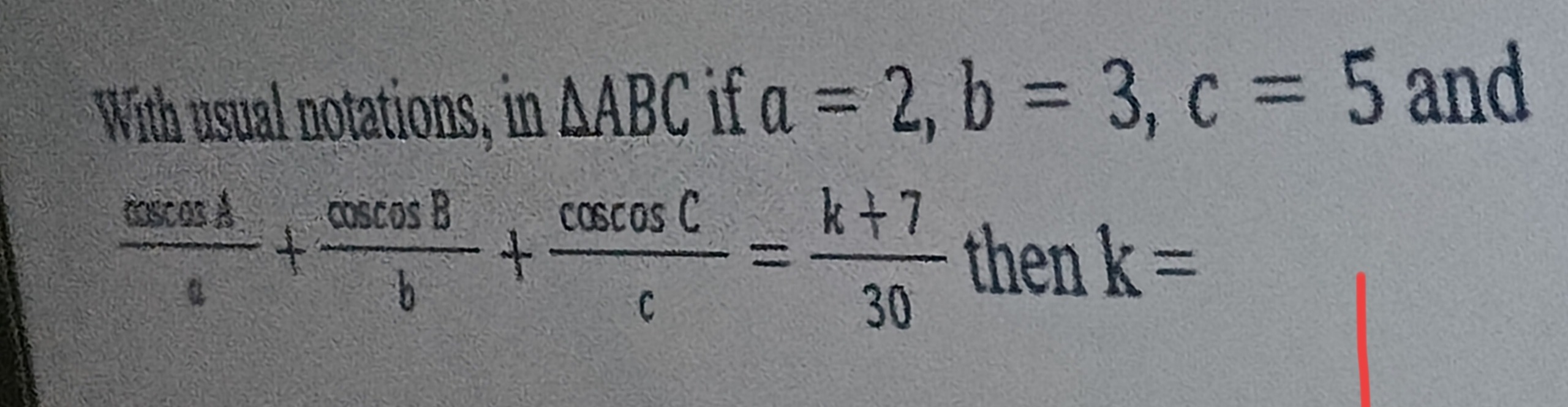
12
Solution
The given problem involves a triangle ABC with side lengths a=2, b=3, and c=5. We need to find the value of k from the given equation:
acosA+bcosB+ccosC=30k+7
First, let's analyze the given side lengths. For a triangle to be formed, the triangle inequality must hold: the sum of the lengths of any two sides must be greater than the length of the third side. Here, a+b = 2+3 = 5. Since c=5, we have a+b=c. This indicates a degenerate triangle, where the three vertices are collinear. Specifically, if A and B are the endpoints of the side c (length 5), then C must lie on the line segment AB such that AC=b=3 and CB=a=2. In this configuration, the angle C (opposite side c) is 180∘, and angles A and B are 0∘.
We can use the cosine rule for each angle: cosA=2bcb2+c2−a2 cosB=2aca2+c2−b2 cosC=2aba2+b2−c2
Substitute these into the expression acosA+bcosB+ccosC: acosA+bcosB+ccosC=a1(2bcb2+c2−a2)+b1(2aca2+c2−b2)+c1(2aba2+b2−c2) To combine these terms, we find a common denominator, which is 2abc: =2abcb2+c2−a2+2abca2+c2−b2+2abca2+b2−c2 =2abc(b2+c2−a2)+(a2+c2−b2)+(a2+b2−c2) =2abca2+b2+c2 This is a general identity for any triangle.
Now, substitute the given values a=2, b=3, c=5 into this identity: a2=22=4 b2=32=9 c2=52=25 a2+b2+c2=4+9+25=38
2abc=2×2×3×5=60
So, the expression becomes: acosA+bcosB+ccosC=6038=3019
We are given that acosA+bcosB+ccosC=30k+7. Equating the two expressions: 3019=30k+7 Multiply both sides by 30: 19=k+7 Solve for k: k=19−7 k=12
