Question
Question: With the usual notation, in \[\Delta ABC\], if \[\angle A + \angle B = 120^\circ ,a = \sqrt 3 + 1\] ...
With the usual notation, in ΔABC, if ∠A+∠B=120∘,a=3+1 and b=3−1. Then, what will be the ratio for ∠A:∠B ?
Explanation
Solution
This question is from Trigonometric geometry. We have to know the angle property for any triangle will be ∠A+∠B+∠C=180∘. By using sine rule property for triangle ABC, we have to show a+ba−bcot2C=tan(2A−B). Then, by putting given values of a and b in this equation we will get ∠A:∠B
Complete step-by-step answer:
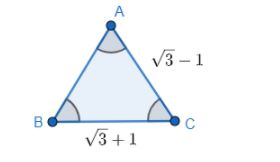
Given, ∠A+∠B=120∘...(i)
