Question
Question: With the help of ray diagram, describe the construction, working of a compound microscope when the f...
With the help of ray diagram, describe the construction, working of a compound microscope when the final image is formed at least distance of distinct vision (D = 25 cm). Derive an expression for magnifying power (m).
Solution
Hint: As a compound microscope is formed by the combination of two convex lenses, we will first find out the magnification by first lens and then with the second lens. After that we will multiply both the magnification to get the magnifying power of the microscope.
Complete step by step solution:
A compound microscope is an optical instrument composed of two short focal lengths convex lenses, which is used for magnifying images of very tiny objects up to 1000 times.
The principle of working of a compound microscope is that when a very small object is placed just away from the focus of an objective lens, an inverted, virtual and highly magnified image is formed. The image formed is at the least distance of distinct vision from the eye piece.
There are two convex lenses in a compound microscope; one is of small aperture, the objective lens O and other is of large aperture, the eye piece E. As the name suggests, the eye piece is held close to the eye and objective piece towards the object. The focal length of both the convex lens is short, still the objective lens focal length is a little shorter. The objective lens has aperture and focal length larger, so as to receive more light rays from the object needed to be magnified and form a bright fringe.
We can draw the schematic diagram of a compound microscope as follows,
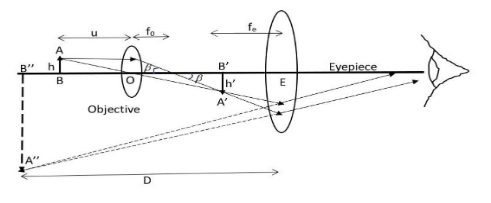
The image formed by the objective is real, inverted and magnified and which serves as an object for the eyepiece. This object is then magnified by the eyepiece to produce the final image which is virtual, inverted and enlarged. The first image formed is near the focal plane of the eyepiece and at a distance appropriate for the final image to form at infinity.
We will first find the linear magnification done by the objective, using tanβ=f0h=foh’
Thus, we have mo=hh’=f0L ………. (i)
Where, h is the size of object, h’ is the size of first image, fo is the focal length of objective, L is the distance between the focal length of objective and eyepiece and is called the tube length of the compound microscope.
Now, we will use a simple microscopic magnification equation to find out the angular magnification me=feD ………. (ii)
Where, D is the distance of the final image from the eyepiece and fe is the focal length of the eyepiece.
Now, total magnification after the image formed at infinity will be m=mo×me=foL×feD
Hence the final image formed can be seen by our eyes held close to the eyepiece and after adjusting the final image to the least distance of distinct vision that is D = 25 cm.
Note: The eyepiece and the objective should be adjusted as such that we get the first image between the focus and optical centre of the eyepiece so as to get the final image at the least distance of the distinct vision. We should draw the ray diagrams following the rules or else may lead to a lot of confusion later.
