Question

With the help of a circuit diagram, explain the working of a Colpitt’s oscillator.

Answer 1

An oscillatory circuit, also called a tank circuit is an electronic circuit that produces a repetitive waveform with a constant amplitude and frequency and the oscillator does not require an external input signal. The tank circuit of a Colpitt’s oscillator consists of two capacitors in series and an inductance coil connected parallel to them.

Formulas used:
The frequency of oscillations of a tank circuit is given by, $f = \dfrac{1}{{2\pi \sqrt {LC} }}$ where $L$ is the inductance of the inductor coil and $C$ is the capacitance of the tank circuit.
The effective capacitance of two capacitors $C_1$ and $C_2$ connected in series is given by, $\dfrac{1}{C} = \dfrac{1}{{C_1}} + \dfrac{1}{{C_2}}$.

Complete Step by Step Answer:
Step 1: Sketching the circuit diagram of the Colpitt’s oscillator.

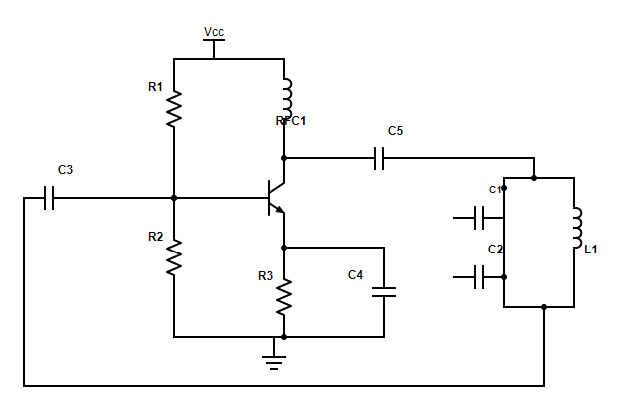
Step 2: Listing the elements of the circuit.
The tank circuit is made up of the two capacitors $C_{1}$ and $C_{2}$ in series and connected parallel to the inductor $L_{1}$.
Between the collector and the $+ V_{cc}$ , a radio frequency choke $RFC_{1}$ is connected. The $RFC_{1}$ acts as a collector load and ensures proper bias to the collector. All ac signals that could be present in the power supply are also decoupled by the radio frequency choke.
The resistors $R_{1}$ and $R_{2}$ form the voltage divider component of the circuit.
The collector capacitor $C_{5}$ couples the oscillatory circuit to the collector, the base capacitor $C_{3}$ blocks the dc currents from entering the base and the emitter capacitor $C_{4}$ bypasses the emitter resistance $R_{2}$.
Step 3: Explanation of the working of the circuit.
The capacitors $C_{1}$ and $C_{2}$ get charged when we switch on the circuit. They discharge through the inductance coil $L_{1}$. An oscillatory current is then produced. The oscillations across $C_{2}$ are feedback to the input of the circuit. The input given to the transistor gets amplified. The output of the transistor will be received across the capacitor $C_{1}$. The process then repeats and leads to the generation of a sustained oscillating output across the secondary coil of the transformer. The primary coil of the transformer is the inductance coil $L_1$.
The frequency of the oscillations of the output will match the natural frequency of the oscillatory circuit (or tank circuit).
The frequency of the tank circuit is given by, $f = \dfrac{1}{{2\pi \sqrt {L_1 \times C} }}$
where $L_1$ is the inductance of the inductor coil and $C$ is the effective capacitance of the capacitors connected in series.
We have the effective capacitance of the tank circuit as $\dfrac{1}{C} = \dfrac{1}{{C_1}} + \dfrac{1}{{C_2}}$.
On simplifying the above expression we get, $C = \dfrac{{C_1C_2}}{{C_1 + C_2}}$
Thus the frequency of the oscillations will be $f = \dfrac{1}{{2\pi \sqrt {L_1 \times \left( {\dfrac{{C_1C_2}}{{C_1 + C_2}}} \right)}}}$

Note:
For an oscillator, the phase difference between the output signal and the input signal must be 0° or 360°. This is referred to as positive feedback. There exists a phase difference of 180° between the output and the input as the ends of the tank circuit are oppositely charged. Also, the transistor used as an amplifier again produces a phase shift of 180° between the output and the input. Thus the total phase difference between the output and input will be 360°.