Question
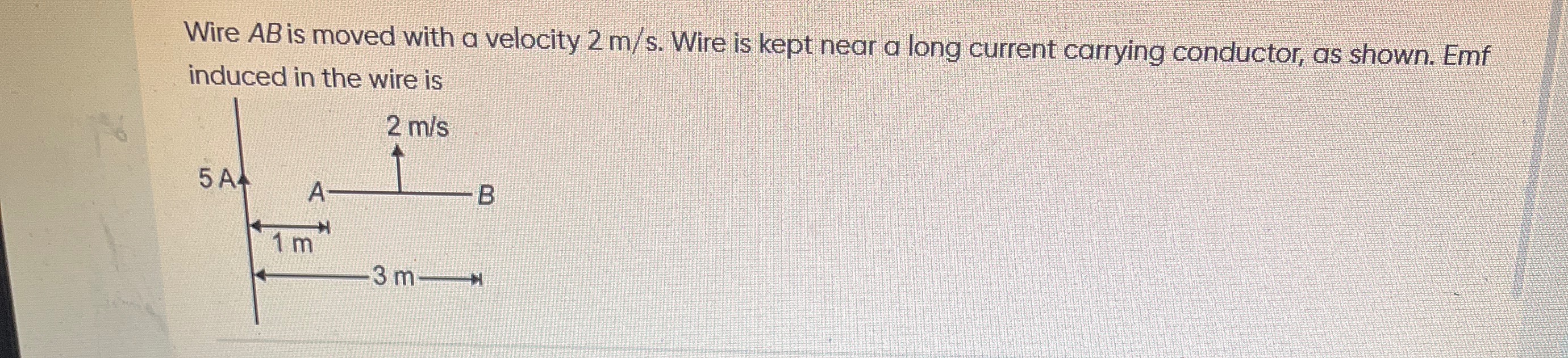
Question: Wire $AB$ is moved with a velocity 2 m/s. Wire is kept near a long current carrying conductor, as sh...
Wire AB is moved with a velocity 2 m/s. Wire is kept near a long current carrying conductor, as shown. Emf induced in the wire is
2 x 10^{-6} ln(4) V
Solution
The problem involves calculating the motional electromotive force (EMF) induced in a conductor moving in a non-uniform magnetic field.
-
Magnetic Field due to the Long Wire:
A long straight current-carrying conductor produces a magnetic field given by the formula: B=2πrμ0I where μ0=4π×10−7 T m/A is the permeability of free space, I is the current (5 A), and r is the perpendicular distance from the wire.
Using the right-hand thumb rule, for an upward current, the magnetic field to the right of the wire is directed into the page. -
Motional EMF:
The wire segment AB has a length L=3 m and is moving with a velocity v=2 m/s upwards. The wire A is at a distance r1=1 m from the long wire, and wire B is at r2=r1+L=1+3=4 m from the long wire.
Since the magnetic field B depends on the distance r, it is not uniform along the length of the wire AB. Therefore, we must integrate to find the total induced EMF.
Consider a small segment dr of the wire AB at a distance r from the long current-carrying wire. The magnetic field at this segment is B(r)=2πrμ0I.
The velocity v is perpendicular to the magnetic field B (velocity is vertical, magnetic field is into the page) and also perpendicular to the length element dr of the wire (velocity is vertical, dr is horizontal).
The induced EMF across this small segment is dE=B(r)vdr.
The total induced EMF across the wire AB is the integral of dE from r1 to r2: E=∫r1r2B(r)vdr Substitute B(r): E=∫r1r2(2πrμ0I)vdr E=2πμ0Iv∫r1r2r1dr E=2πμ0Iv[lnr]r1r2 E=2πμ0Iv(lnr2−lnr1) E=2πμ0Ivln(r1r2) -
Substitute the values:
- μ0=4π×10−7 T m/A
- I=5 A
- v=2 m/s
- r1=1 m
- r2=4 m
E=2π(4π×10−7)×5×2ln(14) E=(2×10−7×5×2)ln(4) E=(20×10−7)ln(4) E=2×10−6ln(4) V
Using ln(4)=2ln(2)≈2×0.693=1.386: E=2×10−6×1.386 E=2.772×10−6 V
Polarity:
Using the right-hand rule for the force on positive charge carriers F=q(v×B):
v is upwards. B is into the page. v×B points to the left (towards the long wire).
This means positive charges are pushed towards point A, making A at a higher potential than B.
The final answer is 2×10−6ln(4) V.
Explanation of the solution:
The magnetic field due to the long current-carrying wire is non-uniform, varying inversely with distance. The motional EMF is calculated by integrating B(r)vdr over the length of the wire AB. The integral leads to E=2πμ0Ivln(r1r2). Substituting the given values I=5 A, v=2 m/s, r1=1 m, and r2=4 m yields the induced EMF.
