Question

Width of a slab is $6cm$ whose $\mu = \dfrac{3}{2}$ . If its rear surface is silvered and the object is placed at a distance $28cm$ from the front face. Calculate the final position of the image from the silvered surface.

Answer 1

As we look at the silvered surface from the rarer medium (air) through the denser medium (slab), the silvered surface will be virtually shifted towards us. i.e., the virtual silvered surface will look closer than that of the actual position of the silvered surface.

Formula used:
The apparent shift of a medium $= d\left( {1 - \dfrac{1}{\mu }} \right)$.
Where, $d$ and $\mu$ are the thickness and refractive index of the medium.

Complete step by step solution:
It is given that,
The width of the slab is $t = 6cm$.
Refractive index of the slab $\mu = \dfrac{3}{2}$
The rear surface of the slab is silvered.
An object is placed at a distance $u = 28cm$ from the front face of the slab.
It is required to find the final position of the image from the silvered surface.
Find the apparent shift of the slab
Let’s draw the diagram to understand better.

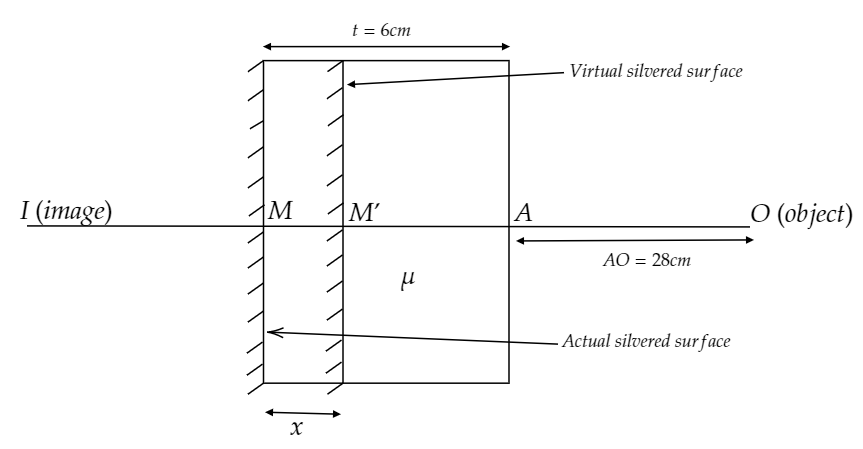
Let $x$ be the apparent shift of the given slab.
We know the formula of apparent shift $x = t\left( {1 - \dfrac{1}{\mu }} \right)$.
Substitute the values of $t$ and ${\mu _0}$ in the above formula.
$x = 6\left( {1 - \dfrac{1}{{\dfrac{3}{2}}}} \right)$
Further calculating, we got
$\Rightarrow x = 2cm$
The position of the virtual silvered surface from the front face is $t' = t - x$
Or $t' = \left( {6 - 2} \right)cm = 4cm$
Step 3 of 3 (Calculate the distance of the image from silvered surface)
The distance of the object from the virtual silvered surface is $u' = t' + u$.
Or $u' = \left( {4 + 28} \right)cm$
Or $u' = 32cm$
We know that the distance of an object from a mirror is equal to the distance of the image from the mirror.
The distance of the image from the virtual silvered surface is $v' = u' = 32cm$.
The distance of the image from the actual silvered surface is $v = v' - x$.
Or $v = \left( {32 - 2} \right)cm$
Or $v = 30cm$
Hence, the image will form at a distance $30cm$ from the actual silvered surface.

Note:
The apparent shift of an object in a given medium is due to the refraction of light. When the ray of light travels from a rarer medium to a denser medium, the refracted ray bends towards the normal i.e., the angle of refraction is smaller than the angle of incidence. So, an object in a given denser medium looks closer to an observer than the actual position of the object as seen from a rarer medium.