Question

Why is the width of the central maxima double in case of diffraction? If possible, derive it mathematically?

Answer 1

In the above question we are basically asked to prove that the width of the central maxima is double in case of diffraction. The width of the central maxima is nothing but the difference between the positions of the first two minima. Hence we will use the expression for the position of minima and accordingly obtain the expression of the width of central maxima and secondary maxima.
Formula used:
$\theta =\dfrac{\lambda }{a}$

Complete step-by-step solution:

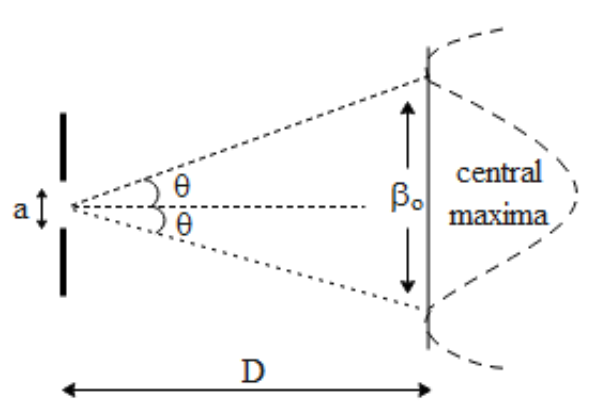
In the above diagram, we can see that the central maxima are subtended at an angle equal to $2\theta$and with slit width equal to a. The angular width of the central maxima is the angular separation between the directions of the first minima on the two sides of the central maxima.
The directions of the first minima on the either side of the of central maxima is given by,
$\theta =\dfrac{\lambda }{a}$ where $\lambda$ is the wavelength of light used. The angular width of the central maxima from the above figure is equal to $2\theta =\dfrac{2\lambda }{a}$
Hence the linear width i.e. ${{\beta }_{\circ }}$ from the above figure is equal to,
$\begin{aligned} & 2\theta =\dfrac{Arc}{radius}=\dfrac{{{\beta }_{\circ }}}{D} \\\ & {{\beta }_{\circ }}=D\times 2\theta \\\ & \Rightarrow {{\beta }_{\circ }}=\dfrac{2D\lambda }{a}...(1) \\\ \end{aligned}$
In case of the secondary maxima, the angular width of the nth secondary maxima is the angular separation between directions of the nth and (n+1)th minima. Direction of nth minima ${{\theta }_{n}}=n\dfrac{\lambda }{a}$. Further the direction of the nth minima is given by, ${{\theta }_{n+1}}=(n+1)\dfrac{\lambda }{a}$. Since the angular width of the secondary maxima is the successive difference between two nth minima we get angular width (W)as,
$\begin{aligned} & W={{\theta }_{n+1}}-{{\theta }_{n}}=(n+1)\dfrac{\lambda }{a}-n\dfrac{\lambda }{a} \\\ & \Rightarrow W=n\dfrac{\lambda }{a}-n\dfrac{\lambda }{a}+\dfrac{\lambda }{a} \\\ & \Rightarrow W=\dfrac{\lambda }{a} \\\ \end{aligned}$
Since linear width is the product of angular width($\beta$ ) times the distance between the screen and slit we get $\beta$ as,
$\begin{aligned} & \beta =W\times D \\\ & \Rightarrow \beta =\dfrac{D\lambda }{a}...(2) \\\ \end{aligned}$
From equation 1 and 2 we can conclude that,
${{\beta }_{\circ }}=2\beta$
Therefore the width of the central maxima is twice that of secondary maxima.

Note: In diffraction, the width of the successive maxima is half of that of the central maxima. It is also to be noted that the intensity of the successive maxima keeps on decreasing. A distinct diffraction pattern is only possible if the slit is very narrow.