Question

Why is the s-orbital always spherical in shape?

Answer 1

Orbitals of all kinds are only mathematical functions that explain certain standing-wave patterns that may be displayed on a graph but have no physical existence. Two or more orbitals (i.e., two or more functions) can be joined both in-phase and out-of-phase to create a pair of resulting orbitals that must have squares that describe real electron distributions in the atom or molecule to be functional.

Complete answer:
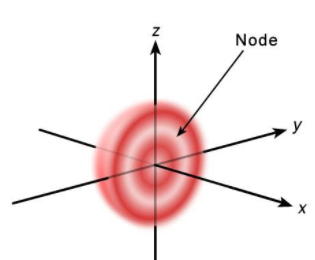
Although the electron is a quantum particle with no fixed position, its orbital may be described as the region of space around the nucleus where the chance of detecting the electron exceeds some arbitrary threshold number, such as 90% or 95%. The orbital corresponds to a standing-wave pattern in 3-dimensional space that we can frequently express more clearly in a 2-dimensional cross-section due to the wave-like nature of matter.
The solitary s-orbitals with l =0 have a sphere-like form. Each single s-orbital is formed of spherically symmetric surfaces that are nested shells for n = 1 (it is most dense at the centre and fades exponentially outwards), but for n = 2 or more, it is basically a solid ball (it is most dense at the centre and fades exponentially outwardly) (i.e., the "wave-structure" is radial, following a sinusoidal radial component as well). At right, you can see a cross-section of these stacked shells. For all n numbers, the s-orbitals are the only orbitals having an anti-node (a area of high wave function density) near the nucleus' centre.
It can be shown that the exact centre of the drum membrane vibrates most strongly in all modes similar to s orbitals, corresponding to the antinode in all s orbitals of an atom. This antinode indicates that the electron is most likely to be at the physical position of the nucleus (which it goes straight through without scattering or hitting), because it is travelling the fastest (on average) at that point, giving it the most momentum.

Note:
A mental "planetary orbit" picture that most closely resembles the behaviour of electrons in s orbitals, all of which have no angular momentum, could be a Keplerian orbit with an orbital eccentricity of 1 but a finite major axis, which is not physically possible (because particles would collide), but can be imagined as a limit of orbits with equal major axes but increasing eccentricity.