Question

Why is the cosine of an obtuse angle negative?

Answer 1

An angle $\phi$ , which is greater than the right angle, i.e. $\phi > 90^\circ$ but less than the straight angles i.e. $\phi < 180^\circ$ is called as an obtuse angle. Hence, an obtuse angle is$90^\circ < \phi < 180^\circ$ .
The cosine of an obtuse angle is negative because of the range of the cosine function which is between 1 and -1. Therefore, when the cosine function completes its half cycle, it is at the middle of 1 and -1, that is 0. Thus, as a result when the cosine function reaches further the half cycle, it crosses 0 from the positive direction and becomes less than 0 i.e. negative.

Complete step-by-step answer:
The cosine functions, or $\cos \theta$ for an angle $\theta$ is a trigonometric function whose range is defined as $\left( { - 1,1} \right)$ i.e.
$\Rightarrow - 1 < \cos \theta < 1$ $\forall \theta$
The cosine function is positive only in the first and the fourth quadrant.
This is why for an obtuse angle, where $\theta < 90^\circ$
$\Rightarrow \cos \left( {90^\circ + \theta } \right) = - \sin \theta$
Which is a negative real number because sine function positive for $\theta < 90^\circ$ .
For example,
$\Rightarrow \cos 120^\circ = \cos \left( {90^\circ + 30^\circ } \right)$
That gives,
$\Rightarrow \cos 120^\circ = - \sin 30^\circ$
i.e.
$\Rightarrow \cos 120^\circ = - \dfrac{1}{2}$
We can also understand this by plotting the graph of a cosine function.

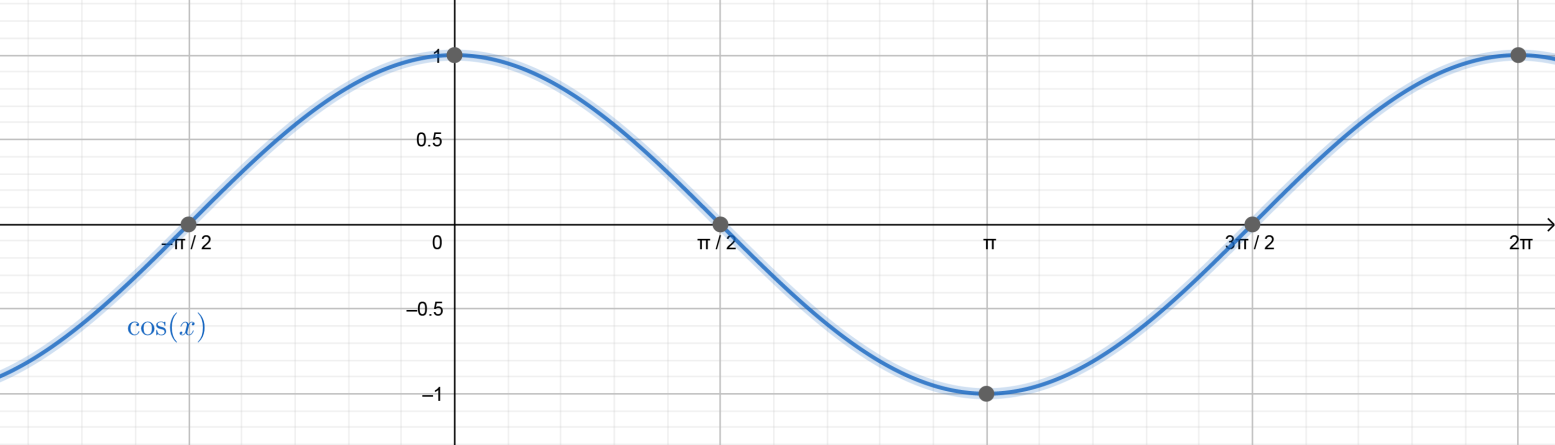
We can see that the cosine function is positive before $\dfrac{\pi }{2}$ and then crosses $0$ downwards at $\dfrac{\pi }{2}$ and becomes negative for obtuse angles i.e. between the values $\left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right)$ and therefore oscillates everywhere between $\left( { - 1,1} \right)$ .

Note: In a right-triangle, cosine function is defined as the ratio of the length of the adjacent side to that of the longest side i.e. the hypotenuse. Suppose a triangle ABC is taken with AB as the hypotenuse and $\theta$ as the angle between hypotenuse and base. Then,
$\Rightarrow \cos \theta = Base/Hypotenuse$
The cosine function is one of the three main primary trigonometric functions (sine, cosine and tangent) and it is itself the complement of the sine function.