Question

Why is the area under the Velocity time graph the distance?

Answer 1

The displacement of moving objects with constant velocity is equal to the product of the object velocity and the amount of time the object is in motion.
We need a velocity-time graph when the object’s velocity gets changed.
The area under the velocity-time graph is known as displacement.

Complete step-by-step solution:
Let us draw the distance-time graph of the body from the position ${x_1}$ and ${x_2}$ as drawn below,

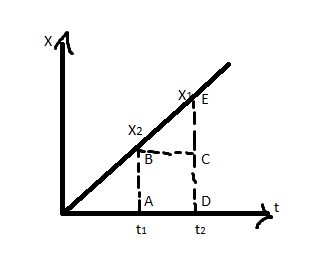
In the above diagram, the area under the curve is equal to the area of the triangle $BCE$ and the area of the rectangle ABCD, this can be expressed as follows,
$A = (AB \times AD) + (\dfrac{1}{2} \times BC \times CE)$
Then this equation becomes,
$A = ({x_1})({t_2} - {t_1}) + \left( {\dfrac{1}{2}({t_2} - {t_1})({x_2} - {x_1})} \right)$
We have to solve the above equation then it becomes,
$A = ({t_2} - {t_1})\left( {{x_1} + \dfrac{1}{2}{x_2} - \dfrac{1}{2}{x_1}} \right)$
After simplification the equations are,
$A = ({t_2} - {t_1})\left( {\dfrac{{{x_1} + {x_2}}}{2}} \right)$
In the above equations When we consider the unit of term on the right-hand side, it gives
$A = meter \times \sec$
From this area under the distance-time graph gives nothing, Now draw the graph of the velocity of the body concerning the time

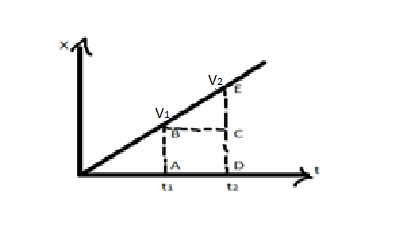
The expression for the area under the curve is as follows,
$A = (AB \times AD) + (\dfrac{1}{2} \times BC \times CE)$
The equation becomes,
$A = ({v_1})({t_2} - {t_1}) + \left( {\dfrac{1}{2}({t_2} - {t_1})({v_2} - {v_1})} \right)$
after solving the above equation,
$A = ({t_2} - {t_1})\left( {{v_1} + \dfrac{1}{2}{v_2} - \dfrac{1}{2}{v_1}} \right)$
Hence it becomes,
$A = ({t_2} - {t_1})\left( {\dfrac{{{v_1} + {v_2}}}{2}} \right)$
In the above equation, the right-hand side determines the unit we get,
$A = \dfrac{{meter}}{{\sec }} \times \sec$
$A = meter$
Here, the area under the curve of the velocity-time graph gives the distance covered by the object

Note: The velocity of the body is determined by the gradient curve in the distance-time graph.
The acceleration of the body is determined by the gradient curve in the velocity-time graph.
By integrating the curve we can calculate the area under the curve.