Question: Why does the vertical line test work?...

Question

Why does the vertical line test work?

Answer 1

Solution

The vertical line test is a method that is used to determine whether a given relation is a function or not. The vertical line test supports the definition of a function. That is, every $x$ value of a function must be paired to a single $y$ value. If we think of a vertical line as an infinite set of $x$ values, then intersecting the graph of a relation at exactly one point by a vertical line implies that a single $x$ value is only paired to a unique value of $y$ .

Complete step by step answer:
Let us understand the given problem using a few examples.
Example 1: Let us draw a graph of the mathematical relation $y = x$
The relation $y = x$ represents a straight line. Also, let us draw some vertical lines on the graph of this line. So, on drawing its graph, we have

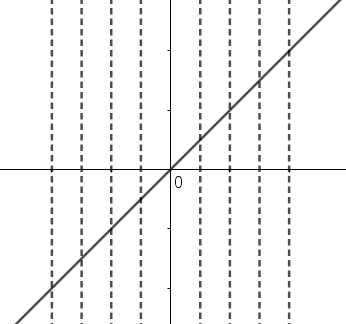
As we can see that there are no lines which are cutting the graph at more than one point. So, for a single value of $x$ there is only one value of $y$ .
Therefore, we can say that the relation $y = x$ is a function.

Example 2: Now, let us draw a graph of another mathematical relation $x = {y^2}$
The relation $x = {y^2}$ represents a parabola. Also, let us draw some vertical lines on the graph of this line. So, on drawing its graph, we have

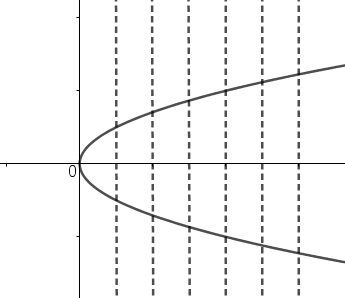
As we can see that there are many lines which are cutting the parabola at more than one point, that is they are cutting the parabola at two points. So, for a single value of $x$ there are two values of $y$ .
Therefore, we can say that the relation $x = {y^2}$ is not a function.
Therefore, it is clear from the above two examples, that the vertical line test verifies a function has an unique output $y$ with each unique input $x$ .

Note:
Remember that if the vertical line intersects the graph more than once this suggests that a single $x$ value is being associated with more than one value of $y$ . This condition causes the relation to be “disqualified” or not considered as a function. Also, if a vertical line intersects the graph in all places at exactly one point, then the relation is a function.