Question

Why and how the intercept of x and y in this equation are negative?
$2x + 3y + 19 = 0$.

Answer 1

To determine the x-intercept, we set y equal to zero and solve for x. Similarly, to determine the y-intercept, we set x equal to zero and solve for y.

Complete step-by-step answer:
Given equation is $2x + 3y + 19 = 0$
To find x-intercept:
Set $y = 0$
$2x + 3y + 19 = 0$

$$\Rightarrow 3y = - 2x - 19 \\\ \Rightarrow 0 = - 2x - 19 \\\ \Rightarrow 19 = - 2x \\\ \Rightarrow x = \dfrac{{ - 2}}{{19}} \\\$$

Thus x-intercept is negative.

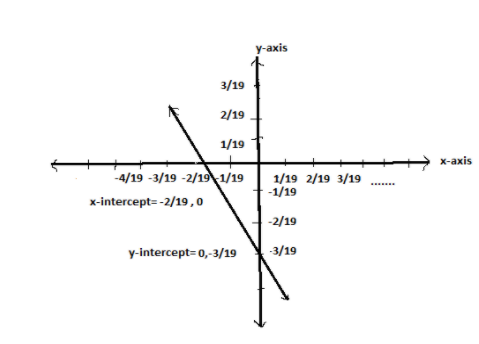
To find y-intercept:
Set $x = 0$
$2x + 3y + 19 = 0$

$$\Rightarrow 2x = - 3y - 19 \\\ \Rightarrow 0 = - 3y - 19 \\\ \Rightarrow 19 = - 3y \\\ \Rightarrow y = \dfrac{{ - 3}}{{19}} \\\$$

Thus y-intercept is negative.

Note: Intercepts are related to lines.
The intercepts of a graph are points at which the graph crosses the axes.
The x-intercept is the point at which the graph crosses the x-axis. At this point, the y-coordinate is zero.
The y-intercept is the point at which the graph crosses the y-axis. At this point, the x-coordinate is zero.