Question

While travelling from one station to another, a car travels $75\,km$ North, $60\,km$ North-East and $20\,km$ East. The Minimum distance between the two stations is
A. $72\,km$
B. $112\,km$
C. $132\,km$
D. $155\,km$

Answer 1

In order to solve this question we need to understand the definition of distance and displacement. Distance is the max gap that a person travels from one place to another it is measured in m whereas displacement is the shortest distance that person covers between two points. Also displacement is always less than or equal to distance but it cannot be greater than distance.

Complete step by step answer:
While travelling from one point to another lets us mark points so that motion could be traced easily. It can be shown like this

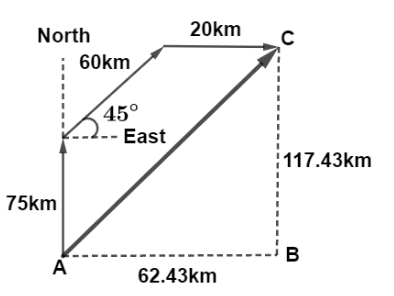
Here A is the initial point of the journey and C is the final point. We calculate displacement BC by resolving it in two directions: the first is the distance covered in the north and other is distance covered in east. So the distance covered in North is ${d_1} = (60\sin 45 + 75)\,km$
$\Rightarrow {d_1} = 117.43\,km$
And the other is distance travelled in east is AB ${d_2} = (60\cos 45 + 20)\,km$
$\Rightarrow {d_2} = 62.43\,km$
From right angle triangle ABC, using Pythagoras theorem, we have
$AC = \sqrt {{{(AB)}^2} + {{(BC)}^2}}$
on putting the values $AC = d$ $AB = {d_2} = 62.43\,km$ and $BC = {d_1} = 117.43\,km$ we get,
$AC = \sqrt {{{(117.43)}^2} + {{(62.43)}^2}}$
So the displacement covered is $d = \sqrt {{{(117.43)}^2} + {{(62.43)}^2}}$
$\therefore d = 132\,km$

So the correct option is C.

Note: It should be remembered that displacement is vector quantity so we can resolve it in two directions and later by using vector rule we can find out the magnitude of displacement. So here we can also observe that displacement is less than distance total covered. This relation is always true. Since a vector quantity has both magnitude and direction so here also we can calculate what is the direction of the final point from starting.