Question

While driving along an unbanked circular road, a two-wheeler rider has to lean with the vertical. Why is it so? With what angle the rider has to lean? Derive the relevant expression. Why is such a leaning not necessary for a four-wheeler?

Answer 1

When a two-wheeler turns around a circular unbanked road, an unbalanced force acts which can cause the two-wheeler to topple. In the case of a four-wheeler, this unbalanced force is also present but it is counterbalanced by a couple formed between normal reaction on outer wheels and its weight.

Complete step-by-step solution:
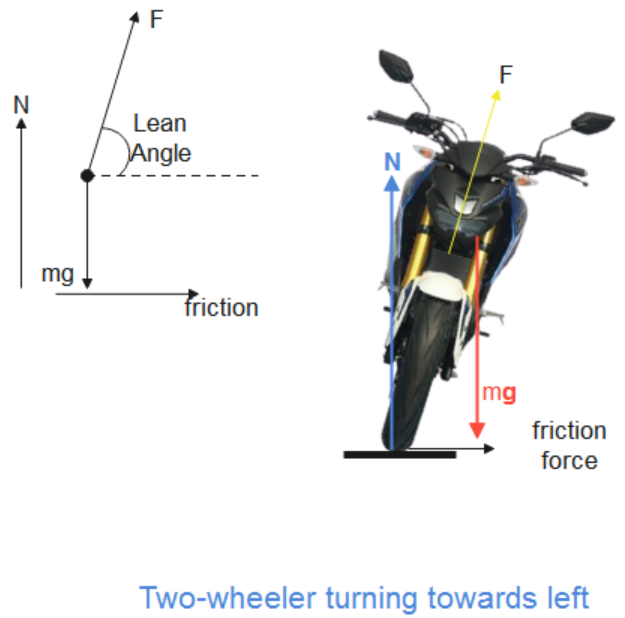
When a two-wheeler rider takes a turn on an unbanked road, the frictional force ${{f}_{s}}$ provides the centripetal force. The normal reaction $N$ of the road is vertically up. If the two-wheeler rider does not lean inward, there will be an unbalanced outward torque equal to ${{f}_{s}}h$ due to the friction force that will topple the two-wheeler rider outward. Therefore, The two-wheeler rider must lean inward to counteract this torque such that the opposite inward torque of the couple formed by $\vec{N}$ and the weight $m\vec{g}$
While turning around a circular unbanked road, the centripetal force is provided by the force of friction. That is,
${{f}_{s}}=\dfrac{m{{v}^{2}}}{r}$
If the two-wheeler rider leans by an angle $\theta$ to the vertical, then, the angle between $\vec{N}$ and $\vec{F}$ is given by
$\tan \theta =\dfrac{{{f}_{s}}}{N}=\dfrac{\dfrac{m{{v}^{2}}}{r}}{mg}=\dfrac{{{v}^{2}}}{gr}$
Therefore, the two-wheeler rider must lean by an angle $\theta =ta{{n}^{-1}}\left( \dfrac{{{v}^{2}}}{gr} \right)$ in order to avoid toppling.

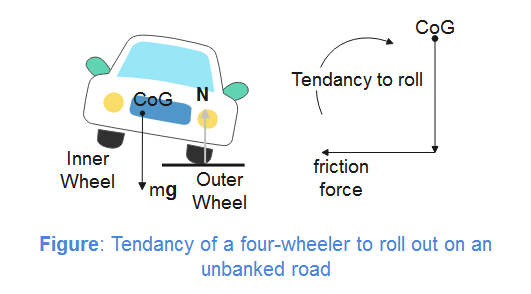
When a four-wheeler takes a turn along an unbanked road, it also has a tendency of skidding outwards. But in a four-wheeler, when the inner wheels get lifted above the ground, it is counterbalanced by a restoring torque due to a couple formed by the normal reaction on outer wheels and its weight.

Note: While turning around a circular unbanked road, the centripetal force is provided by the force of friction. Both centripetal and centrifugal forces are in the opposite direction.
For a safe turn, the centripetal force must be greater than or equal to the centrifugal force.