Question

Which sample A or B has a shorter mean life?

Answer 1

Mean life, in radioactivity, average lifetime of all the nuclei of a particular unstable atomic species. This time interval may be thought of as the sum of the lifetimes of all the individual unstable nuclei in a sample, divided by the total number of unstable nuclei present.

Complete step-by-step solution:
The mean life of B is shorter than that of A
According to the Radioactive Decay Law states that the decay rate of a nucleus is given by the formula of
$\dfrac{{dN}}{{dt}} = - \lambda N$
Where,
$\dfrac{{dN}}{{dt}}$ is the rate of decay of the nucleus with respect to time, $\lambda$ is the decay rate constant of the nucleus and $N$ is the number of nuclei present in the sample. As shown in the graph the X axis the decay rate and Y axis is the time of decay, now to point the decay rate constant in the graph we have to draw a slope on the curve of sample A and B like this

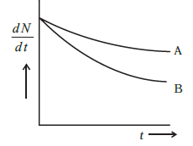
The slope of the A and B curve dedicates the decay rate constant of the sample A and B respectively. Now as for the mean life of the samples, the mean life formula is
$\tau = \dfrac{1}{\lambda }$
Where,$\tau$is the mean life and $\lambda$ is the decay rate constant. So according to the diagram the mean life of A and B are given as
${\tau _A} = \dfrac{1}{{{\lambda _A}}},{\tau _B} = \dfrac{1}{{{\lambda _B}}}$
${\lambda _A} < {\lambda _B}$
${\tau _A} > {\tau _B}$
Now as we can see in the above diagram (in the explanation), the value of decay rate constant of B and A is ${\lambda _A} < {\lambda _B}$ (the flatter the curve the lesser is the slope therefore, the value of the slope of B is greater than A as the curve of B is greater than A) respectively. Hence, due to inverse proportionality the value of mean life of B is lesser than that of A.
Therefore, the mean life of B is shorter than that of A.

Note: We need to remember that radioactive decay (also known as nuclear decay, radioactivity, radioactive disintegration or nuclear disintegration) is the process by which an unstable atomic nucleus loses energy by radiation. A material containing unstable nuclei is considered radioactive.