Question

Which one of the following statements is true?
A) $\cos \left( {A + B} \right) = \cos A + \cos B$
B) $\cos \left( {A + B} \right) = \cos A\cos B$
C) $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$
D) $\cos \left( {A + B} \right) = \cos A\cos B + \sin A\sin B$

Answer 1

Hint : In this question, we need to find which of the above given statements is true. For this, we will consider a rotating line in an anti-clockwise direction, which makes acute angles $a$ and $b$ . By which we will construct a diagram and we will find the angles of the points. And use the formula of $\sin \theta$ and $\cos \theta$ to find which of the above statements are true.

Complete step-by-step answer :
Let a rotating line $OX$ rotate about $O$ in the anti-clockwise direction. From starting position to its initial position $OX$ making an acute angle $a$ . And again, the rotating line rotates further in the same direction and starting from position $OY$ and makes out an acute angle $b$ .
To understand this concept, let us construct a figure.
First draw a horizontal line $X$ (the x-axis) and mark the origin $O$ . Next, draw a line $Y$ from $O$ at an angle $a$ above the horizontal line $X$ and in the similar way, draw a second line $Z$ at an angle $b$ above that. Such that, the angle between the line $Z$ and the x-axis is $a + b$ . Here, $a$ and $b$ are positive acute angles and $a + b < 90^\circ$ .
Mark the point $P$ in the line $Z$ (which is defined by the angle $a + b$ ) at a unit distance from the origin.
Let $PQ$ be a line, perpendicular to the line $OQ$ defined by angle $a$ , which is drawn from point $Q$ on this line to point $P$ . Therefore, $OQP$ forms a right angle.
Let $QA$ be a perpendicular from point $A$ on the x-axis to $Q$ and $PB$ be a perpendicular from point $B$ on the x-axis to $P$ . Therefore, $OAQ$ and $OBP$ are right angles.
Now, draw $R$ on $PB$ such that $QR$ is parallel to the x-axis.

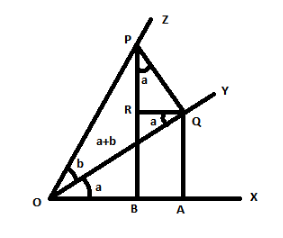
From the diagram, $OQA = \dfrac{\pi }{2} - a$
Then, $RQO = a$
$\Rightarrow$ $RQP = \dfrac{\pi }{2} - a$
Then, $RPQ = a$
Therefore, $RPQ = \dfrac{\pi }{2} - RQP$
$= \dfrac{\pi }{2} - \left( {\dfrac{\pi }{2} - RQO} \right)$
= $RQO$
= $a$
Now from the right-angled triangle $POB$ , we get,
$\cos (a + b) = \left( {\dfrac{{OB}}{{OP}}} \right)$
$= \dfrac{{OA - BA}}{{OP}}$
$= \dfrac{{OA}}{{OP}} - \dfrac{{BA}}{{OP}}$
$= \dfrac{{OA}}{{OP}} - \dfrac{{RQ}}{{OP}}$
$= \dfrac{{OA}}{{OQ}}.\dfrac{{OQ}}{{OP}} - \dfrac{{RQ}}{{PQ}}.\dfrac{{PQ}}{{OP}}$
We know that,
$\sin \theta = \dfrac{{Opposite}}{{Hypotenuse}}$
And, $\cos \theta = \dfrac{{Adjacent}}{{Hypotenuse}}$
By using the above formula, we get,
$\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b$
Hence, option C) $\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$ is the true statement.
So, the correct answer is “Option C”.

Note : In this question, be careful in applying the formula of $\sin \theta$ and $\cos \theta$ when using the diagram. In similar way, we can find the values of $\sin \left( {a + b} \right)$ , $\sin \left( {a - b} \right)$ and $\cos \left( {a - b} \right)$ . We can also use complementary angle formulae i.e., $\sin \theta = \cos \left( {\dfrac{\pi }{2} - \theta } \right)$ and $\cos \theta = \sin \left( {\dfrac{\pi }{2} - \theta } \right)$ to determine $\cos \left( {a + b} \right)$ . Here, consider $\theta = \left( {a + b} \right)$ and apply it in the formula of $\cos \theta$ and solve it.