Question

Which one of the following species does not exist under normal conditions?
A.$B{e_2}^ +$
B.$B{e_2}$
C.${B_2}$
D.$L{i_2}$

Answer 1

This question could be approached using MOT which stands for molecular orbital theory in which the number of electrons in BMO (Bonding Molecular Orbital) and in ABMO (Antibonding Molecular Orbital) can be used to calculate the bond order of the molecule, which decides the stability of the molecule.

Complete Step by step solution:
The bond order is the number of bond of bond which is present in between two atoms, which can be calculated using number of electrons in BMO and ABMO by the formula given below:
Bond order = $\dfrac{1}{2}({N_B} - {N_A})$, where ${N_B}$ stands for the number of electrons in the BMO and ${N_A}$ stands for the number of electrons in the ABMO. Now we can draw the MO diagram of $B{e_2}$ and find outs bond order.

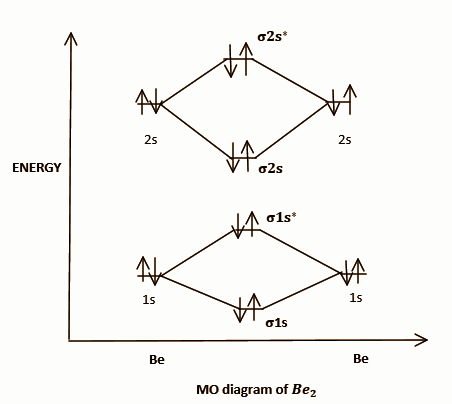
$Be$ electronic configuration is:$1{s^2}2{s^2}$.
This diagram can be represented by equation given as follows:
$\sigma 1{s^2}{\sigma ^*}1{s^2}\sigma 2{s^2}{\sigma ^*}2{s^2}$ , where $\sigma$ stands for the sigma bonds between atoms which are single bonds and $*$ represents the antibonding orbitals. Now, we have a total of four electrons in bonding and 4 electrons in antibonding orbitals. So using the formula:
Bond order= $\dfrac{1}{2}({N_B} - {N_A})$= $\dfrac{1}{2}(4 - 4) = 0$
Since bond order is $0$ it means there is no bond between two $Be$ atoms and hence the $B{e_2}$ molecule will be unstable. For other options we can similarly draw the molecular orbital diagrams and can find out the bond order.
For $B{e_2}^ +$ one electron will be removed from the antibonding orbital and hence ${N_B} = 4$ and ${N_A} = 3$. So the bond order $= \dfrac{1}{2}({N_B} - {N_A}) = \dfrac{1}{2}(4 - 3) = \dfrac{1}{2}$. This means there is a partial bond between them and hence stable.
For $Li$ the electronic configuration is $1{s^2}2{s^1}$ and the $L{i_2}$ molecular orbital can be written by the equation $\sigma 1{s^2}{\sigma ^*}1{s^2}\sigma 2{s^2}$ and the bond order will be $\dfrac{1}{2}({N_B} - {N_A}) = \dfrac{1}{2}(4 - 2) = 1$ which means there is a single bond between them, so stable.
For $B$ the electronic configuration is $1{s^2}2{s^2}2{p^1}$ and the ${B_2}$ molecular orbital will be written by the equation $\sigma 1{s^2}{\sigma ^*}1{s^2}\sigma 2{s^2}{\sigma ^*}2{s^2}\pi 2{p_x}^1\pi 2{p_y}^1$ . So, ${N_B} = 6$ and ${N_A} = 4$ and bond order is $\dfrac{1}{2}(6 - 4) = 1$ and hence there is single bond between two boron atoms and hence boron molecule will be stable.

Note: In case of boron atom it involves $p$ orbitals and all the three $p$ orbitals ${p_x}, {p_y}, {p_z}$ are not equivalent while electrons are filled, ${p_x}, {p_y}$ have lower energy than ${p_z}$ where total electrons of the molecule are $14$ or less than $14$.