Question

Which one of the following geometries (i.e. shapes) is not possible for the $s{p^3}{d^2}$ hybridization?
A.Capped octahedral
B.Octahedral
C.Square planar
D.Square pyramidal

Answer 1

$s{p^3}{d^2}$ hybridization has 1s, 3p and 2d orbitals taking part and intermixed to form six identical hybrid orbitals. These six orbitals (might include lone pairs) are placed towards the corners of an octahedron, inclined at 90 degrees to one another.

Complete step-by-step solution:
Hybridization is defined as mixing of two atomic orbitals with equal energy levels to give a degenerated new hybrid orbital. It is the process in which redistribution of orbital energy of individual atoms takes place to form orbitals of equivalent energy.
Atomic orbitals undergo hybridization when they have equal energy. Thus, the number of hybrid orbitals formed is equal to the number of atomic orbitals that underwent mixing. The shape of the molecule can be predicted easily if the hybridisation of the molecule is known.
Based on the nature of mixing of orbitals, hybridisation is classified as sp , $s{p^2}$ , $s{p^3}$ , $s{p^3}d$ , $s{p^3}{d^2}$ and $s{p^3}{d^3}$ .
Considering octahedral geometry, the six atoms are arranged around a central atom at the corners of an octahedron. Four out of six hybrid orbitals lie in one plane while the other two are directed above and below the plane perpendicularly. $s{p^3}{d^2}$ hybridization is formed when electron from ground state of $n{s^2}n{p^4}$ jumps to an excited state of $n{s^1}n{p^3}n{d^2}$ , with which six orbitals of ligands are hybridised.
Same as for square planar, four hybrid orbitals are directed at the corners of an octahedron and the two lone pairs of central atoms lie above and below the plane to form $s{p^3}{d^2}$ hybridisation.
Similarly, in square pyramidal, the five atomic orbitals are the same in energy with the lone pair, thus arrange themselves at six vertices of an octahedron and form $s{p^3}{d^2}$ .
But in case of capped octahedron, $s{p^3}{d^2}$ is destroyed by the presence of a lone pair and becomes $s{p^3}{d^3}$ . This can be visualised by the structure shown below. The lone pair is fixed as a cap on the octahedral structure at its top.

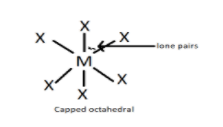
Hence, the correct option is (A).

Note: There is a difference between $s{p^3}{d^2}$ and ${d^2}s{p^3}$ . In $s{p^3}{d^2}$ all the orbitals have the same principal quantum number i.e. n. Such complexes are known as outer orbital complexes as they use outer d-orbital. In ${d^2}s{p^3}$ , the principal quantum number of d orbital changes to $\left( {n - 1} \right)$ , one less than that of s and p orbitals i.e. inner d orbital is used, so such complexes are known as inner orbital complexes.