Question

Which of the functions defined below are one-one function(s)?
A) $f\left( x \right) = x + 1$, $\left( {x \geqslant - 1} \right)$
B) $g\left( x \right) = x + \dfrac{1}{x}$, $\left( {x \geqslant 0} \right)$
C) $h\left( x \right) = {x^2} + 4x - 5$, $\left( {x > 0} \right)$
D) $f\left( x \right) = {e^{ - x}}$, $\left( {x \geqslant 0} \right)$

Answer 1

We know that a function $f\left( x \right)$ is said to be one-one if $f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$ is true only when ${x_1} = {x_2}$. Then we can check these conditions in each of the given functions. The functions which satisfy this condition are one-one and others are not one-one.

Complete step by step solution:
We know that a function $f\left( x \right)$ is said to be one-one if $f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$ is true only when ${x_1} = {x_2}$.
Now consider option A, $f\left( x \right) = x + 1$. It is defined for $\left( {x \geqslant - 1} \right)$.
Now let us take $f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$.
$\Rightarrow {x_1} + 1 = {x_2} + 1$
On simplification, we get
$\Rightarrow {x_1} = {x_2}$
Therefore, the function in option A is one-one.
Now consider option B, $g\left( x \right) = x + \dfrac{1}{x}$. It is defined for $\left( {x \geqslant 0} \right)$.
Now let us take $g\left( {{x_1}} \right) = g\left( {{x_2}} \right)$.
$\Rightarrow {x_1} + \dfrac{1}{{{x_1}}} = {x_2} + \dfrac{1}{{{x_2}}}$
On taking the LCM, we get
$\Rightarrow \dfrac{{{x_1}^2 + 1}}{{{x_1}}} = \dfrac{{{x_2}^2 + 1}}{{{x_2}}}$
As the fractions are equal when denominators and numerators are equal, we can say that
$\Rightarrow {x_1} = {x_2}$
Therefore, the function in option B is one-one.
Now consider option c, $h\left( x \right) = {x^2} + 4x - 5$. It is defined for $\left( {x > 0} \right)$.
Now let us take $h\left( {{x_1}} \right) = h\left( {{x_2}} \right)$.
$\Rightarrow {x_1}^2 + 4{x_1} - 5 = {x_2}^2 + 4{x_2} - 5$
On simplification, we get
$\Rightarrow \left( {{x_1} + 4} \right){x_1} = \left( {{x_2} + 4} \right){x_2}$
As the function is defined for positive numbers, we can say that
$\Rightarrow {x_1} = {x_2}$
Therefore, the function in option C is also one-one.
Now consider option D, $f\left( x \right) = {e^{ - x}}$. It is defined for $\left( {x \geqslant 0} \right)$.
Now let us take $f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$.
$\Rightarrow {e^{ - {x_1}}} = {e^{ - {x_2}}}$
On taking log on both sides, we get
$\Rightarrow - {x_1}\log e = - {x_2}\log e$
On cancelling the common terms, we get
$\Rightarrow {x_1} = {x_2}$
Therefore, the function in option D is one-one.
From the 4 results, we can say that all the given functions are one-one.

So, the correct answers are option A, B, C and D.

Note:
Note: Alternate solution to solve this problem is given by plotting the graph of the function and checking whether the function has the same value for different values of x.
Now consider option A, $f\left( x \right) = x + 1$. It is defined for $\left( {x \geqslant - 1} \right)$.

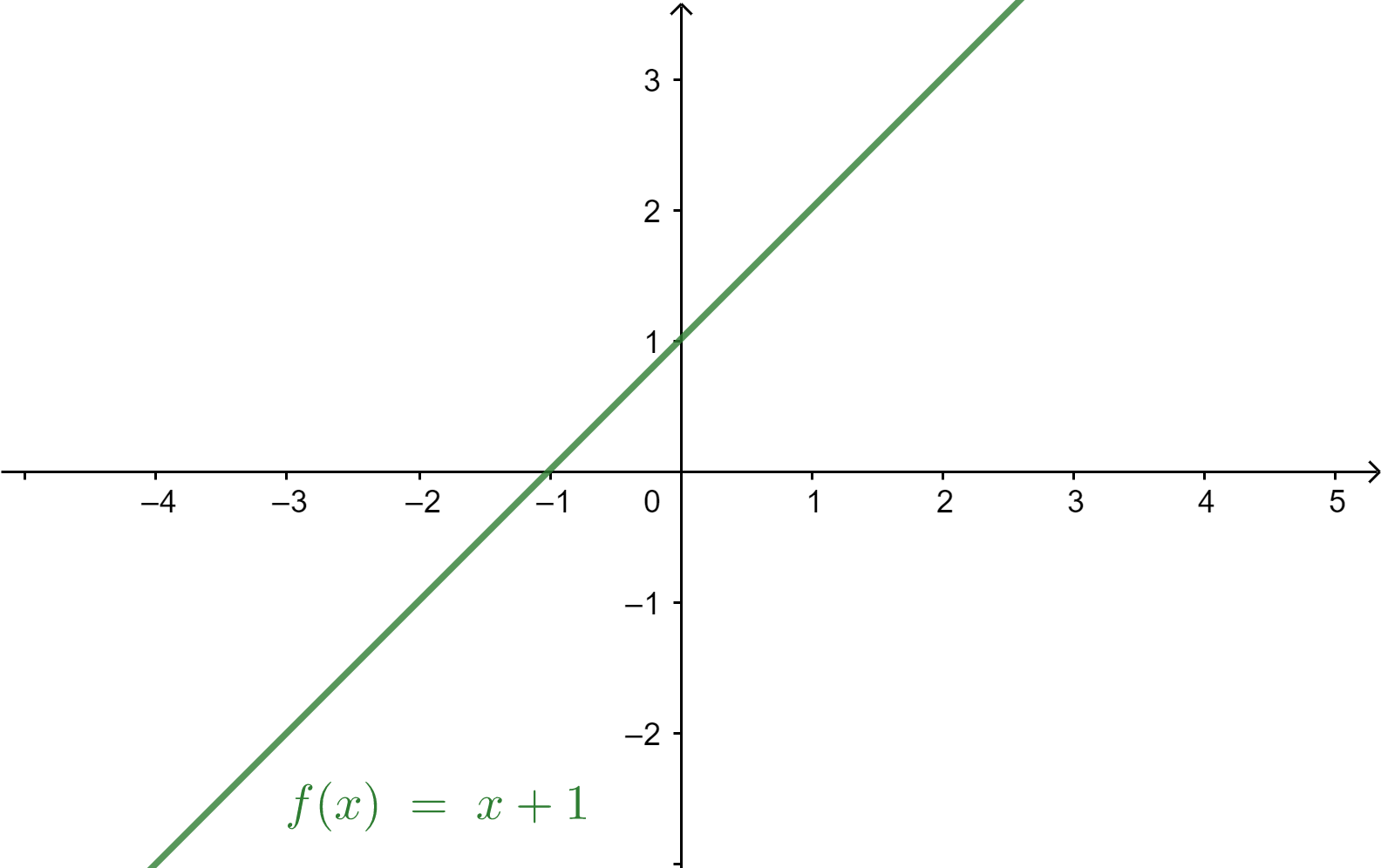
As the graph is linear, there is only one value of x for which the function has the same value. So it is a one-one function.
Now consider option B, $g\left( x \right) = x + \dfrac{1}{x}$. It is defined for $\left( {x \geqslant 0} \right)$.

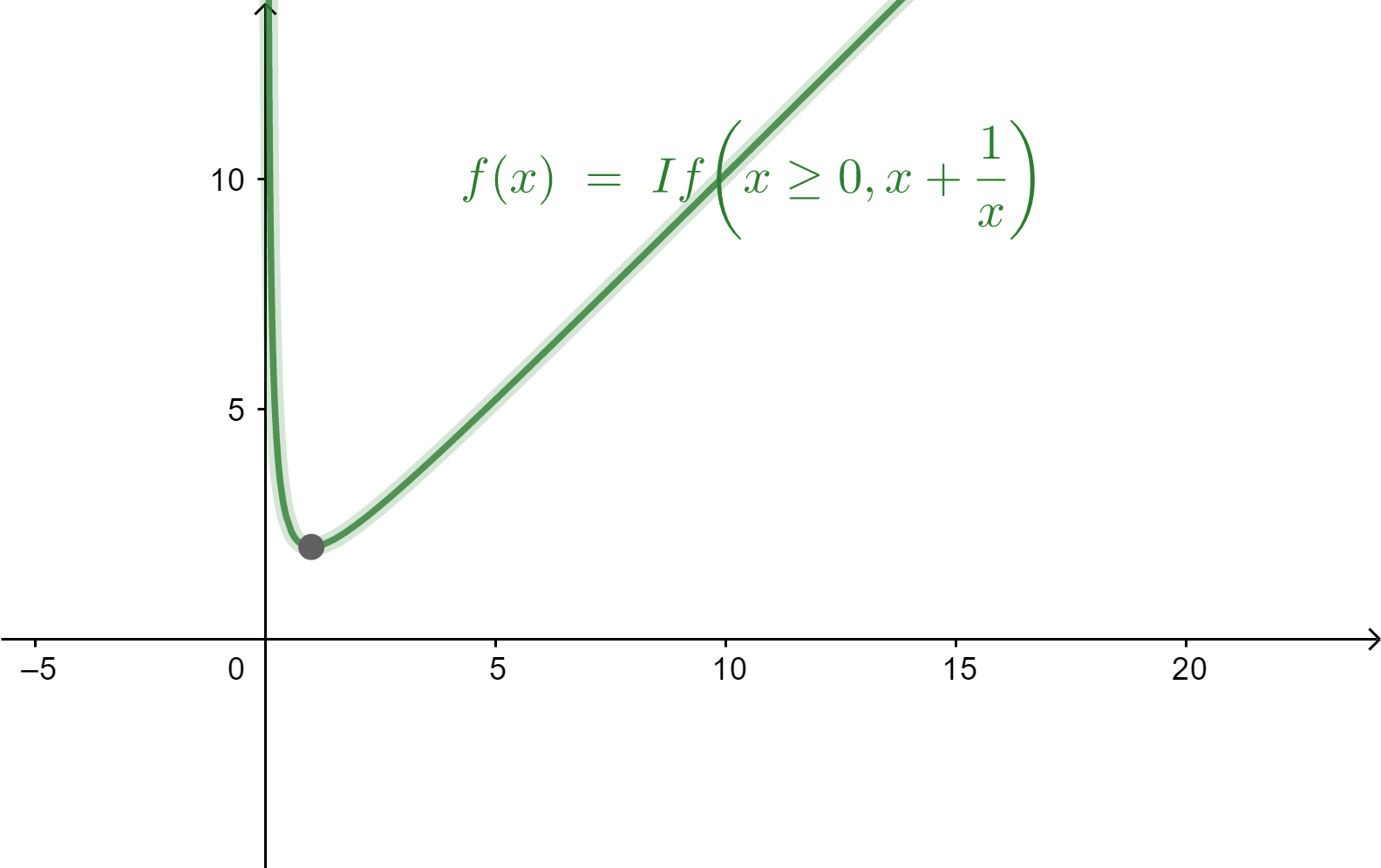
From the graph, we can say that there is only one value of x for which the function has the same value. So, it is a one-one function.
Now consider option c, $h\left( x \right) = {x^2} + 4x - 5$. It is defined for $\left( {x > 0} \right)$.

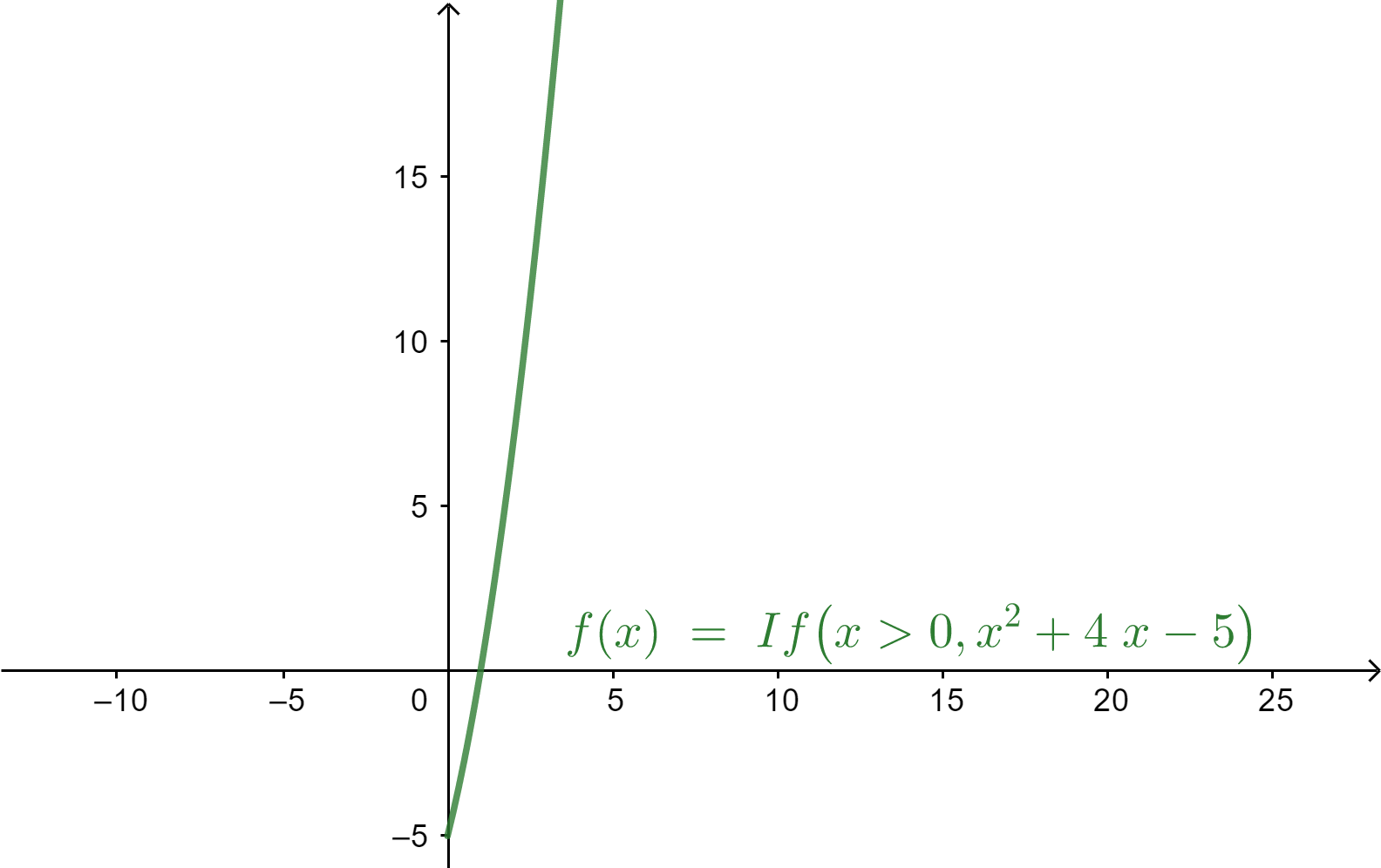
From the graph, we can say that there is only one value of x for which the function has the same value. So, it is a one-one function.
Now consider option D, $f\left( x \right) = {e^{ - x}}$. It is defined for $\left( {x \geqslant 0} \right)$.

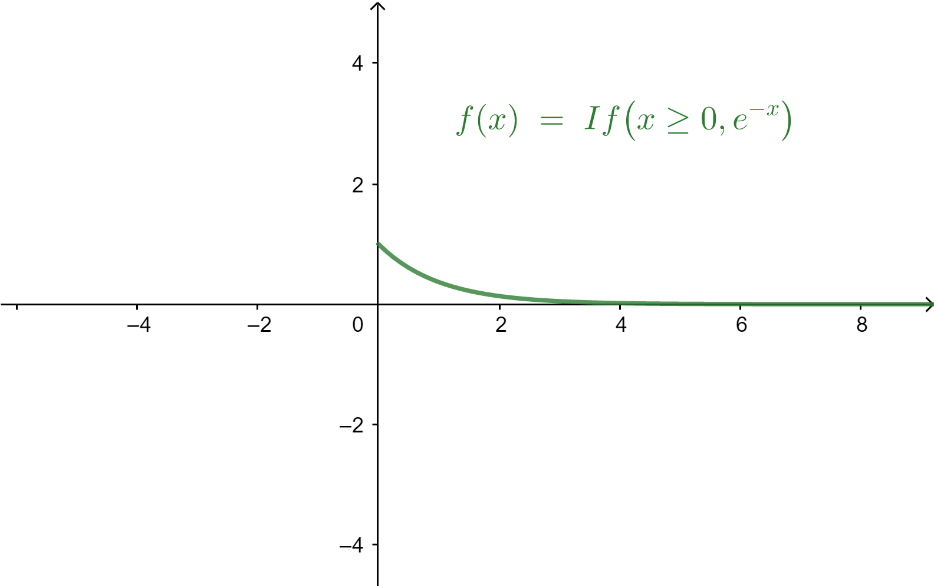
From the graph, we can say that there is only one value of x for which the function has the same value. So, it is a one-one function.
From the 4 results, we can say that all the given functions are one-one.