Question
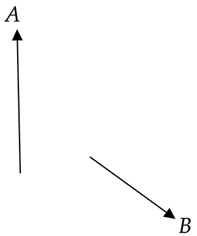
Question: Which of the following vectors best represents the vector \[\overrightarrow{A}+\overrightarrow{B}\] ...
Which of the following vectors best represents the vector A+B ?
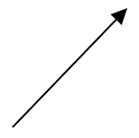
A)
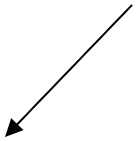
B)
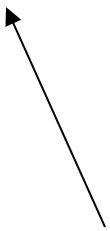
C)
D)
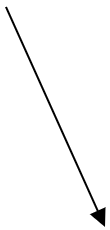
Solution
We all know what vectors are? But let’s brush up our knowledge. Vectors are physical quantities having magnitude as well as a particular direction. Vectors are represented through arrows, as given in the question. The length of the arrow is an indication of the vector’s magnitude and the arrowhead points in the direction of the vector.
Complete step by step solution:
In the given question, we are directed to find the resultant of the addition of the two vectors A and B whose diagrammatic representation has been provided to us.
A common method of finding the sum of vectors is to join the head of one of the given vectors to the tail of the other vector. Now, the resultant vector will have its tail at the tail of the first vector and its head at the head of the second vector. The given vectors and the resultant vector will form a triangle and hence this method of vector addition goes by the name of the triangle law for vector addition. For the given question, the triangle law of vector addition can be shown as follows:
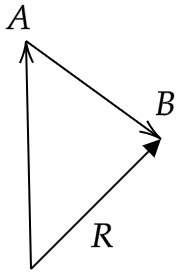
You will see that the tail of the vector B is joined with the head of the vector A and then the resultant vector R has its tail at the tail of the vector A and its head at the head of vector B
Only considering the resultant we can represent it as follows
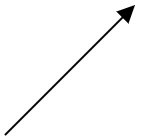
Hence we can say that option (A) is the correct answer and represents the vector A+B.
Note: Students should be careful that while putting the tail of a vector with the head of the other vector, they should not change the magnitude and direction of the original vectors as doing so would furnish them incorrect answers. The triangle law of vector addition has another alternative known as the parallelogram law of vector addition, where the resultant is given as the diagonal of the parallelogram formed by the original vectors.
