Question

Which of the following statements are true and which are false? In each case give a valid reason for saying so
a) p: Each radius of a circle is a chord of the circle.
b) q: the center of the circle bisects each chord of the circle
c) r: circle is a particular case of an ellipse
d) s: if x and y are integers such that x>y then –x< –y
e) t: $\sqrt {11}$ is a rational number

Answer 1

Hint: In order to comment whether it is true or false, first we will take an example then according to the given statement we will proceed further.

Complete step-by-step answer:

a) p: Each radius of a circle is a chord of the circle.
As we know by the definition of chord, it should intersect the circle in two points.

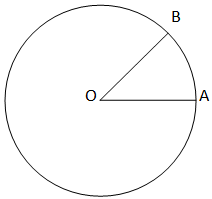
In the given figure OB and OA is radius but they don’t intersect the circle at two points.
So, OB and OA is not the chord of the circle.
Hence, the radius of a circle is not a chord of the circle.
So the statement p is false.

b) q: the center of the circle bisects each chord of the circle.

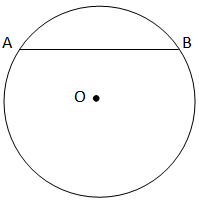
Here in the given figure AB is the chord of the circle as it intersects the circle at 2 points.
But it does not pass through the center O.
Hence, the center of the circle does not bisect each chord of the circle.
So the statement q is false.

c) r: circle is a particular case of an ellipse
As we know that equation of ellipse is given by:
$\dfrac{{{x^2}}}{a^2} + \dfrac{{{y^2}}}{b^2} = 1$
And if in the equation of ellipse we put the value a = b = r we get:
$\dfrac{{{x^2}}}{r^2} + \dfrac{{{y^2}}}{r^2} = 1 \\\ \Rightarrow \dfrac{{{x^2} + {y^2}}}{r^2} = 1 \\\ \Rightarrow {x^2} + {y^2} = {r^2} \\\$
which is the equation of the circle.
Hence, circle is the particular case of ellipse.
So, statement r is true.

d) s: if x and y are integers such that x>y then –x< –y
Given that: x>y
Let us multiply both sides by -1. As we know that if we multiply an inequality by a negative constant then the sign of inequality reverses. So after multiplying by -1 the inequality becomes:
$\Rightarrow \left( { - 1} \right)x < \left( { - 1} \right)y \\\ \Rightarrow - x < \- y \\\$
Hence, if x and y are integers such that x>y then –x< –y
So, the statement is true.

e) t: $\sqrt {11}$ is a rational number
As 11 in not a perfect square so the square root of 11 is not an integer.
So, $\sqrt {11}$ cannot be written in the form of $\dfrac{p}{q}$ which is the basic criterion of rational number.
Hence, $\sqrt {11}$ is an irrational number.
So, the statement t is false.

Note: In order to prove a statement to be false students can do so by just giving an example which rejects the claim made in the statement. But in order to prove a statement to be true a valid reason must be given. In order to solve such types of problems students must remember the basic definitions of shapes and their general formulas.