Question

Which of the following sets are finite and which are infinite?
(1). Set of concentric circles in a plane
(2). Set of letters of the English alphabets
(3)\left\\{ x\in N:x>5 \right\\}
(4). \left\\{ x\in N:x<200 \right\\}
(5). \left\\{ x\in Z:x<5 \right\\}
(6). \left\\{ x\in R: 0 < x < 1 \right\\}

Answer 1

Hint: Finite set means the number of element in any set is countable like set A=\left\\{ a,p,l,e \right\\}, we have 4 elements in set A thus it is an infinite set, and infinite set means the number of element in set is not countable or uncountable. Like set B=\left\\{ x:x\in R:~where\text{ }x\text{ }is\text{ }any\text{ }real\text{ }number \right\\}.

Complete step-by-step answer:

It is given in the question to check if the given set is finite or infinite. Basically finite set means the number of elements in any set is countable like set X=\left\\{ x:x\in EvenNumber:x<10 \right\\} which results in following set members X=\left\\{ 2,4,6,8 \right\\} also infinite set means the elements of set are uncountable, like a set \left\\{ x:x\in even\text{ }number\text{ }:\text{ }x\text{ }is\text{ }any\text{ }even\text{ }number \right\\}.
Now, we will check all the set one by one and if the elements in the set are countable then it is a finite set and if the elements in the set are uncountable then it is infinite.
We have set 1 as a set of concentric circles in a plane.

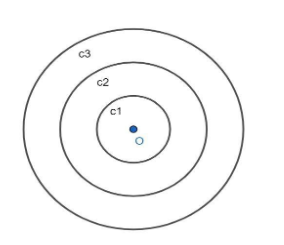
So, we know that concentric circles in a plane means circles have the same common centre and we know we can draw infinite circles with the same centre in a plane, thus the set of concentric circles in a plane is an infinite set.
We have set 2 as the set of letters of the English alphabet. We know that the total number of alphabet is 26 which is countable, thus set 2 is a finite set.
We have set 3 as \left\\{ x\in N:x>5 \right\\}, the given set is in set builder form we will first convert this to roster form \left\\{ 6,7,8,9,10,........ \right\\}. As x is a natural number greater than 5. Since there are uncountable numbers of natural numbers greater than 5, therefore resulting in an infinite set.
We have set 4 as \left\\{ x\in N:x<200 \right\\}. The given set is in set builder form, we will convert it into roster form. As x is a natural number less than 200. We have a countable number of elements in the set, with 199 as the last element in the set, \left\\{ 1,2,3,4....199 \right\\}.Therefore, we have 199 elements in the set, thus it is a finite set.
We have set 5 as \left\\{ x\in Z:x<5 \right\\}. Since x belongs to an integer where x is less than 5. We know that there are an infinite number of integers less than 5, including the negative integers. So, this set is also an infinite set.
We have set 6 as \left\\{ x\in R: 0 < x < 1 \right\\}. Here x belongs to any real number between 0 and 1, and there are an infinite number of real numbers between 0 and 1, therefore this set is an infinite set. Since real numbers can be of any form, we can have an infinite number of real numbers between 0 and 1, even though we have two end limits as 0 and 1.

Note: Many times students are stuck while converting set builder form into roster form. Usually students do not know how to convert set builder form to roster form, thus this raises a problem in solving such problems. Therefore it is recommended to convert set builder form into roster form carefully.