Question
Question: Which of the following represents the magnetic field due to a straight conductor of uniform cross se...
Which of the following represents the magnetic field due to a straight conductor of uniform cross section of radius ‘a’ and carrying a steady current?
A.
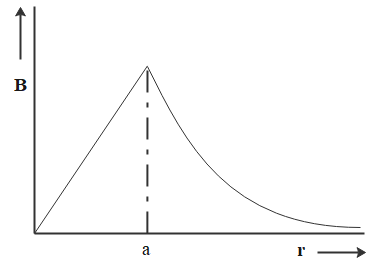
B.
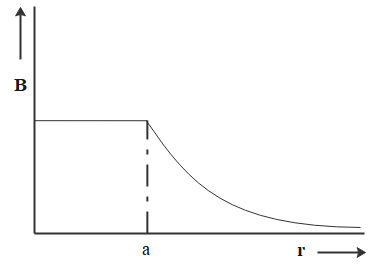
C.
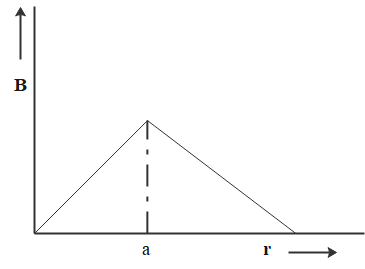
D.
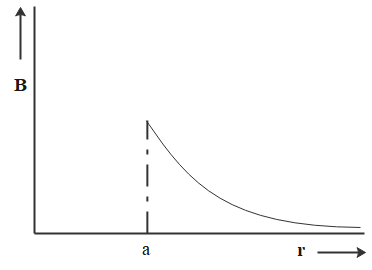
Solution
Use ampere’s law to obtain magnetic fields inside and outside the straight conductor. The variation of magnetic field with respect to its distance from the axis of conductor can be analysed from the expression.
Complete step-by-step answer:
Let us assume that the steady current flowing through the straight conductor is ‘I’. Then, according to ampere’s circuital law magnetic field density along an imaginary circular path around the conductor at perpendicular distance ‘r’ from the axis of the straight conductor is
B=2πrμ0I
This relation is valid only for circles of radius r≥a.
To derive relation for r≤a we assume that the uniform current density in the conductor is J. Then,
J=πa2I
Since, J is constant, the current flowing through a circular cross-section of radius ‘r’ is
I=Jπr2
Where a is the radius of the cross section. Then, according to ampere’s circuital law magnetic field density inside the conductor along an imaginary circular path around the conductor at perpendicular distance ‘r’ from the axis of the straight conductor is
B=2πrμI=2πrμJπr2=2μJr
From the above equation, we can note that the magnetic field inside the conductor is directly proportional to its distance from the axis. We also observed that for a radius of imaginary circular path greater than the radius of cross-section of conductor, the magnetic field intensity is inversely proportional. This corresponds to option A.
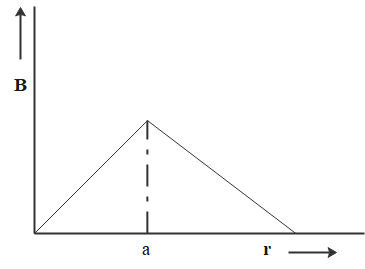
So, the correct answer is “Option A”.
Note: Magnetic field intensity due to a current carrying conductor is linearly proportional to its distance from its axis inside the conductor. But for distances lying outside the conductor, the magnetic field density is inversely proportional to the same.
