Question
Question: Which of the following potential energy curves in the above figures cannot possibly describe the ela...
Which of the following potential energy curves in the above figures cannot possibly describe the elastic collision of two billiard balls? Here r is the distance between the centers of the balls.
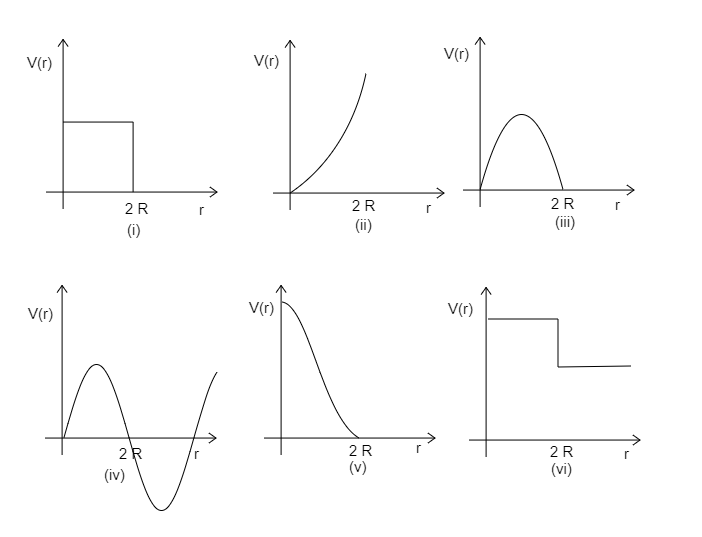
Solution
When the two billiard balls tend to the elastic collision, thus the potential energy of the balls decreases with an increase in the distance between two billiard balls because the potential energy is inversely proportional to the distance between two masses. By using this condition, we can easily determine the correct graph from the given question.
Complete step by step answer:
The potential energy of a system containing two masses is inversely proportional to the distance between the two masses.
V(r)∝r1
Where V(r) is the potential energy and r is the distance between two balls.
The potential energy is a function of position if the collision is an elastic collision. If the two colliding bodies make contact with each other, then the potential energy is zero.
By the given case, a decrease in separation potential energy increases, after the contact of the two bodies with each other.
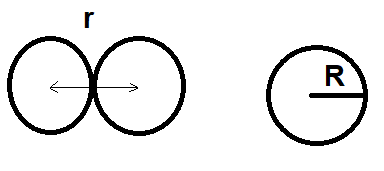
where,
r is the distance between the center point of two balls,
R is the radius of each ball.
Thus,
V=0, for r=2R
As the distance between the two balls increases, the potential energy gradually decreases.
So, the potential energy will become zero (V(r)=0) when two balls make a contact with each other at r=2R
Hence, all other curves cannot possibly deserve the elastic collision of two balls.
So out of the given potential energy curves, only the option (v) curve satisfies these two conditions.
Note:
Potential energy may be converted into the form of motion, called kinetic energy, and in turn to other forms such as electrical energy. The potential energy diagram shows the potential energy of the object depends on its position and shows all kinds of things about the motion of the object.
