Question

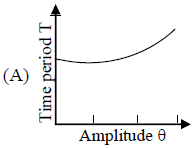
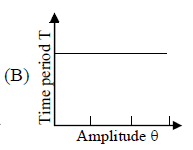
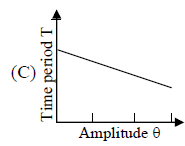
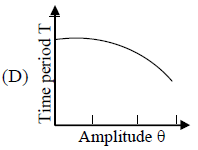
Which of the following plots represents schematically the dependence of the time period of a pendulum if measured and plotted as a function of the amplitude of its oscillations? (Note: amplitude need not be small)

Answer 1

We know the basic formula for calculating the time period of any simple pendulum. But, in our formula we work under the assumption that the oscillations of the simple pendulum are very small and thus we equate the value of theta and sin theta as for very small angles, theta is equal to sin theta. But, for large amplitudes of oscillation, we cannot use this approximation and we shall find the value of the new time period.

Complete step-by-step answer:
Let us understand the forces acting on the bob of the simple pendulum by the given figure:
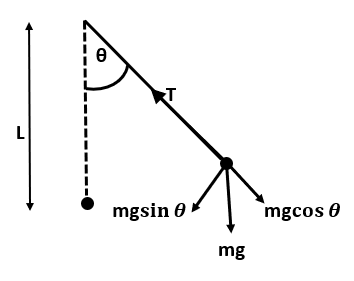Here, we assume that:
The mass of string carrying the bob is negligible and that the friction due to air is also negligible. Then, we can write the equation of force on block as:
$\Rightarrow T-mg\cos \theta =m{{v}^{2}}L$
Also, the torque tending to bring the mass to its equilibrium position can be written as:
$\Rightarrow \tau =mgL\sin \theta$ which is equal to $I\alpha$
Here,
$I$ is the moment of inertia of the bob whose value is equal to $m{{L}^{2}}$ .
Thus, equating these we get:
$\begin{aligned} & \Rightarrow mgL\sin \theta =m{{L}^{2}}\alpha \\\ & \Rightarrow \alpha =\dfrac{g\sin \theta }{L} \\\ \end{aligned}$
We know that,
$\Rightarrow \alpha ={{\omega }^{2}}\theta$
Thus putting this value of $\alpha$ in above equation, we get:
$\begin{aligned} & \Rightarrow {{\omega }^{2}}\theta =\dfrac{g\sin \theta }{L} \\\ & \Rightarrow \omega =\sqrt{\dfrac{g\sin \theta }{L\theta }} \\\ \end{aligned}$
Now, the time period of any oscillation is given by:
$\Rightarrow T=\dfrac{2\pi }{\omega }$
Using the value of angular frequency $(\omega )$ obtained above we can calculate the time period of oscillation as:
$\Rightarrow T=2\pi \sqrt{\dfrac{L}{g}}\sqrt{\dfrac{\theta }{\sin \theta }}$
Here, we can see that the time period of oscillation is directly proportional to the square root of angle of oscillation or Angular amplitude. Thus, the time period of oscillation will increase with the increase in angular amplitude $(\theta )$ .

So, the correct answer is “Option A”.

Note: It should be known to us the different assumptions under which a formula has been derived. Or else, we will end up getting wrong answers. Here, if we would have applied the original formula then we could see that the time period was independent of the Amplitude which is not the case.