Question

Which of the following options is the correct combination?

Column $1$	Column $2$	Column $3$
$(i){W_{1 \to 2}} = \dfrac{1}{{\gamma - 1}}({P_2}{V_2} - {P_1}{V_1})$	$(i)Isothermal$	(P)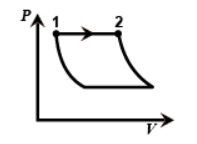
$(ii){W_{1 \to 2}} = - P{V_2} + P{V_1})$	$(ii)Isochoric$	(Q)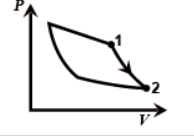
$(iii){W_{1 \to 2}} = 0$	$(iii)Isobaric$	(R)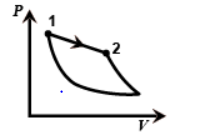
$(iv){W_{1 \to 2}} = - nRT\ln (\dfrac{{{V_1}}}{{{V_2}}})$	$(iv)Adiabatic$	(S)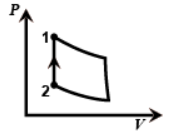

(A).(II)(iv)(P)
(B).(III)(ii)(S)
(C).(II)(iv)(R)
(D).(IV)(ii)(S)

Answer 1

Hint : Now coming on the figure we can see that the first one is the graph of an Isobaric process since pressure is constant throughout from one to two.
In the second one work done is adiabatic as pressure is decreasing rapidly from one to two. So this figure gives us an adiabatic process.
In the third figure the volume is decreasing from one to two so it is an Isothermal process.
And in the last figure the volume is constant from two to one so this is the isochoric process as work done will be zero.

Complete Step By Step Answer:
In the given question we know that work done for adiabatic process is:
${W_{1 \to 2}} = \dfrac{1}{{\gamma - 1}}({P_2}{V_2} - {P_1}{V_1})$
For work to be done by isobaric process:
${W_{1 \to 2}} = - P{V_2} + P{V_1}$
Now work done by isochoric process:
${W_{1 \to 2}} = 0$ . Since the volume is constant throughout the whole process so the work done will be zero.
And last work done by isothermal:
${W_{1 \to 2}} = - nRT\ln (\dfrac{{{V_1}}}{{{V_2}}})$
So if we combine the column first and column second, we get;
$(iii)$ $(ii)$
In the options. That is $(iii){W_{1 \to 2}} = 0$ is the isochoric process.
Now coming on the figure we can see that the first one is the graph of an Isobaric process since pressure is constant throughout from one to two.
In the second one work done is adiabatic as pressure is decreasing rapidly from one to two. So this figure gives us an adiabatic process.
In the third figure the volume is decreasing from one to two so it is an Isothermal process.
And in the last figure the volume is constant from two to one so this is the isochoric process as work done will be zero.
After seeing all the figures and equations we can find that option B is the correct option as this is the only pattern where equation with figure is correctly given that is for isochoric process.
So $(B).(iii)(ii)(S)$ is the correct option.

Note :
Basically in an isochoric process that is sometimes also called a constant-volume process, is a type of thermodynamic process in which volume is constant throughout the process. This is a type of quasi-static- process.
For an adiabatic process that occurs without the transfer of heat.