Question
Question: Which of the following most closely indicates the correct variation of the gravitation potential \(V...
Which of the following most closely indicates the correct variation of the gravitation potential V(r) due to a large planet of radius R and uniform mass density? (the diagrams are not drawn to scale)
A.
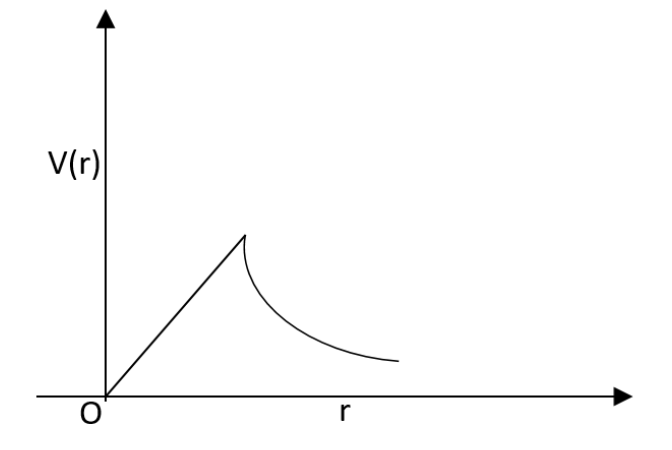
B.
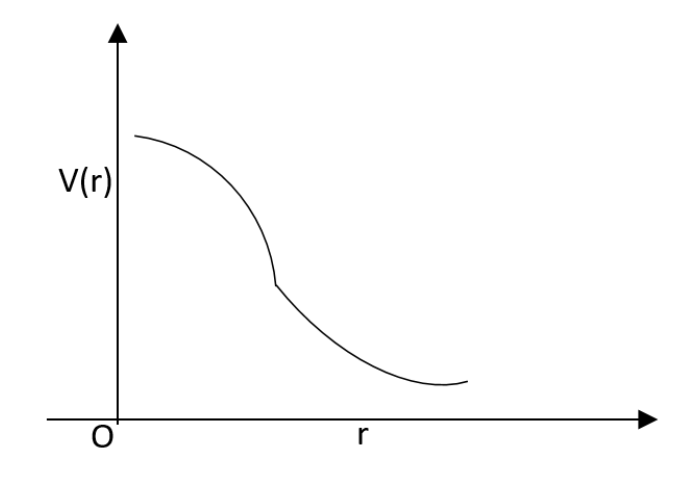
C.
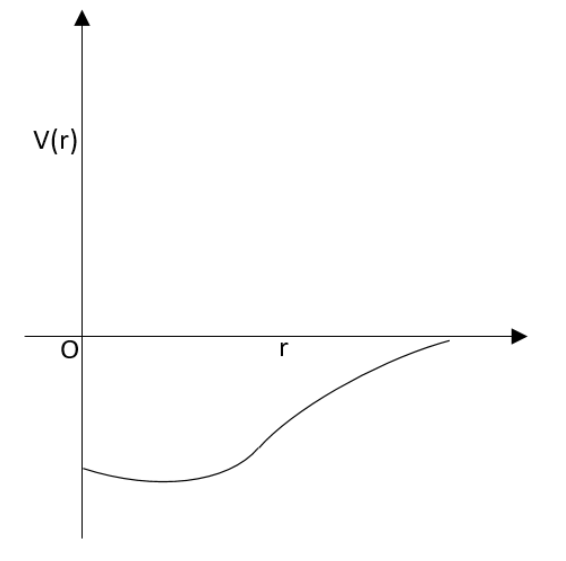
D.
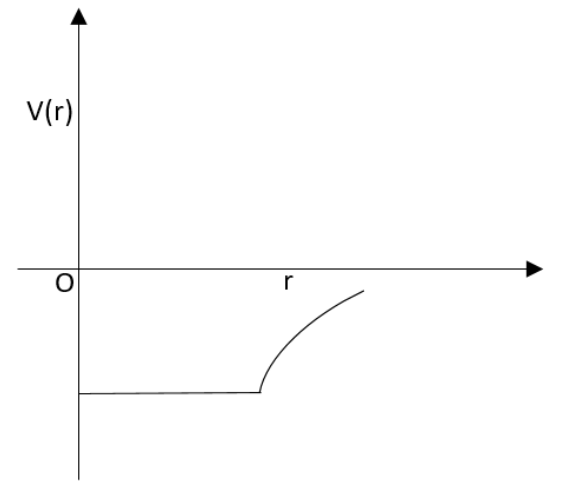
Solution
The potential is expressed by the equation which is the product of the gravitational constant, mass of the planet, the difference between thrice the square of the radius of the planet and the distance from the surface of the planet which is divided by twice the cube of the distance from the surface. This will be helpful in solving the question.
Complete step by step answer:
As the gravitational potential at a height can be expressed as an equation which can be written as,
V(r)=2R3GM(3R2−r2)
Where G be the gravitational constant, M be the mass of the planet, R be the radius of the planet and r be the distance at which the potential has been measured from the surface of the planet.
Using this equation, we can see that the graph C is more closely depicting the variation of the gravitational potential of the planet. Therefore the answer will be more accurate in the case of option C.
So, the correct answer is “Option C”.
Note: The gravitational potential at any specific point will be equivalent to the work per unit mass that has been required to make a body move to that point from a selected reference point. It is similar to the electric potential where the mass is playing the role of charge. Gravitational potential gives us the direction of motion of an object in the gravitational field of another object. This is a scalar quantity which is depending only on the magnitude of the quantity.
