Question

Which of the following is true regarding the symmetry of the function ? $f(x) = x^{4}\ + x^{2}\ + 3$
A. $f(x)\ = f( - x)$
B. $f(x) = - f( - x)$
C. It is an even function.
D. Symmetric wrt y axis

Answer 1

In this question, we need to know which of the given statements is true regarding the symmetry of the given function. First, let us know the concept of symmetry . That is if the given function is even then it is symmetric about the y axis and similarly if the given function is odd then it is symmetric about the x axis. First we need to find whether the given function is even or odd. For that we need to substitute $- x$ in the place of $x$.

Complete step-by-step answer:
Given function $f(x) = x^{4}\ + x^{2}\ + 3$
First we need to find whether the given function is even or odd.
Now we can substitute $- x$ in the place of $x$.
On substituting,
We get,
$\Rightarrow \ f( - x)\ = ( - x)^{4} + ( - x)^{2} + 3$
On simplifying,
We get,
$f( - x) = x^{4}\ + x^{2}\ + 3$
Hence we can tell that $f(x)$ is equal to $f( - x)$
Hence the given function is even.
According to the concept of symmetric, if the given function is even then it is symmetric about y axis
Thus the given function is symmetric about the y axis.

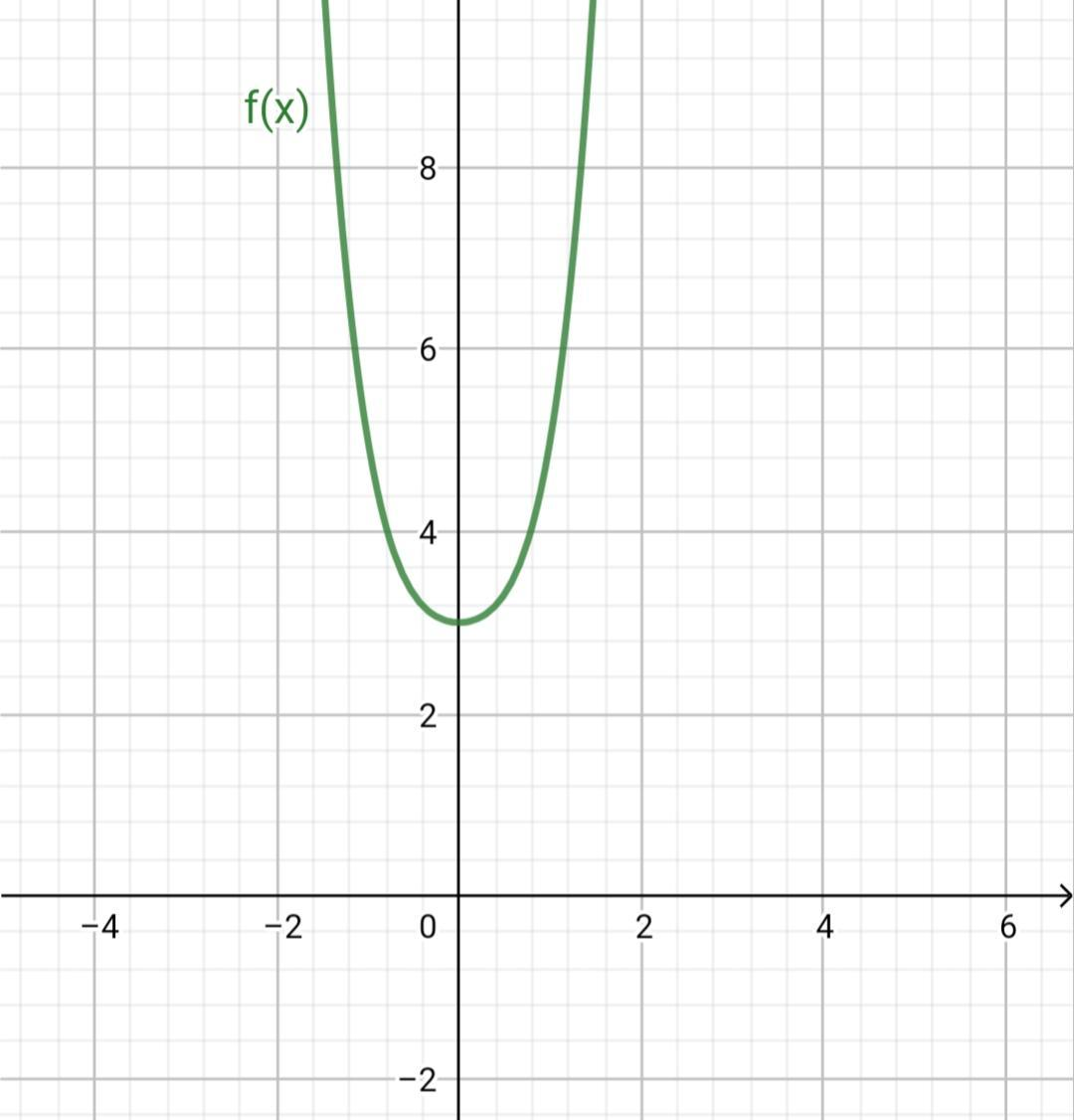
Thus the true statement is $f(x)\ = f( - x)$ , It is an even function and Symmetric wrt y axis.
Final answer :
The true statement is $f(x)\ = f( - x)$ , It is an even function and Symmetric wrt y axis.
Option A, C, D are the true statements.

So, the correct answer is “Option A,C and D”.

Note: In order to solve these types of questions, we should have a strong grip over even and odd functions. If $f(x)$ is equal to $f( - x)$, then the function is said to be the even function similarly if $f(x)$ is equal to $- f( - x)$ then the function is said to be the odd function. We also need to know that if a function is both even and odd, then it is equal to $0$ everywhere it is defined similarly if a function is odd, the absolute value of that function is an even function