Question

Which of the following is the work done by a Centripetal Force?
A) increases by decreasing the radius of the circle
B) decreases by increasing the radius of the circle
C) increases by increasing the mass of the body
D) is always zero

Answer 1

By using the equation of work done to find the work done and consider the force as centripetal force while calculating the total work. And also use the vector dot products to complete the final steps. And also, by using the trigonometric function, the solution is determined.

Formula used:
The formula for finding the Work done by a Force $F$is given by,
$W = \vec F \cdot \vec S$
Where $\vec F$ is the Force acting on the body and $\vec S$ is the displacement.
The circular motion force is acting towards the center and the displacement vector is always perpendicular to the force.

Complete step by step solution:
Here the force is centripetal force so the work done by this centripetal force ${F_c}$
$W = \vec F \cdot \vec S\,............................\left( 1 \right)$
We have the equation to find the dot product of two vector quantities,
$\Rightarrow \vec {\rm A} \cdot \vec {\rm B} = {\rm A}{\rm B}\cos \theta$
Where $\theta$ is the angle between the $\vec A$ and $\vec B$
By taking the dot product on equation $\left( 1 \right)$
$\Rightarrow W = {F_c}S\cos \theta$

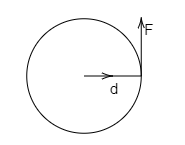
Here in the circular motion and $\vec S$ are perpendicular to each other
There for the angle $\theta = {90^ \circ }$
$\Rightarrow W = {F_c}S\cos 90$
Putting the value of $\theta$ we will get $\cos 90 = 0$
$\Rightarrow W = 0$
Therefore the work done by a centripetal force is always zero.

So, the correct answer is option (D).

Additional information:
The work done is here, the increment or change in kinetic energy of the revolving body. The revolution of electrons around the nucleus is the example for a circular motion and during this circular motion force acting towards the center of the body which is known as the centripetal force.

Note: Here the force and displacement are vector quantities so you have to take the dot product. Also consider the angle made by the force and displacement, while you are taking the dot product. Here, the angle is considered as ${90^ \circ }$, because while the motion of the particle is circular, then the distance and the force are perpendicular to each other.