Question

Which of the following is an onto function: -
(a) $f:\left[ 0,\pi \right]\to \left[ -1,1 \right],f\left( x \right)=\sin x$
(b) $f:\left[ 0,\pi \right]\to \left[ -1,1 \right],f\left( x \right)=\cos x$
(c) $f:R\to R,f\left( x \right)={{e}^{x}}$
(d) $f:Q\to R,f\left( x \right)={{x}^{3}}$

Answer 1

Draw the graph of each of the functions given in the options and check if their range is equal to codomain or not. If their range is equal to the codomain provided then it will be onto function otherwise not.

Complete step-by-step solution
Here, we have been provided with four options containing four functions with their domain and codomain. We have to check which of these functions is an onto function.
Now, we know that an onto function is a function whose range is equal to its codomain given. We have several methods to determine the range of a function but here we will use the graphical method to determine the range. So, let us check each option one – by – one.
(i) $f:\left[ 0,\pi \right]\to \left[ -1,1 \right],f\left( x \right)=\sin x$
Here, we have the function $\sin x$ and its co – domain is [-1, 1]. Drawing the graph of $\sin x$ for the domain [0, $\pi$], we have,

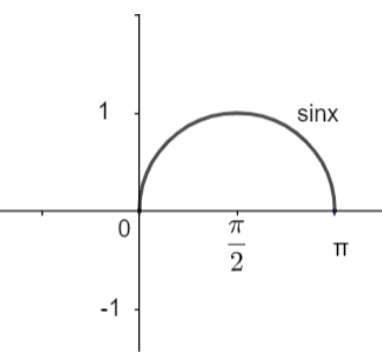
Clearly, we can see that the range of $\sin x$ for the given domain is [0, 1] which is not equal to the codomain [-1, 1]. Hence, $\sin x$ is not an onto function.
(ii) $f:\left[ 0,\pi \right]\to \left[ -1,1 \right],f\left( x \right)=\cos x$
Here, we have the function $\cos x$ and its co – domain is [-1, 1]. Drawing the graph of $\cos x$ for the domain [0, $\pi$], we have,

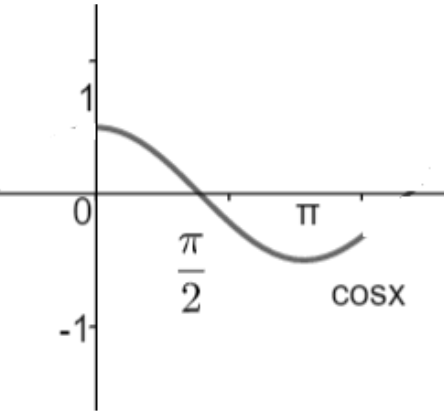
Clearly, we can see that the range of $\cos x$ for the given domain is [-1, 1] which is equal to the codomain [-1, 1]. Hence, $\cos x$ is an onto function.
(iii) $f:R\to R,f\left( x \right)={{e}^{x}}$
Here, we have the function ${{e}^{x}}$ and its codomain is R, that is all real numbers. Drawing the graph of ${{e}^{x}}$ for the domain R, we have,

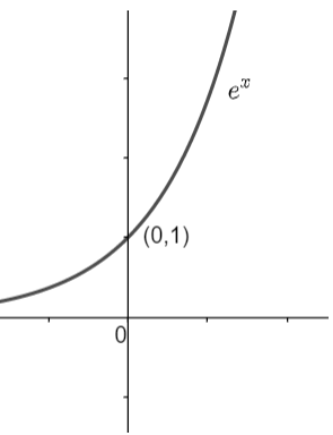
Clearly, we can see that the range of ${{e}^{x}}$ for the given domain is (0, $\infty$) which is unequal to the codomain R. Hence, ${{e}^{x}}$ is not an onto function.
(iv) $f:Q\to R,f\left( x \right)={{x}^{3}}$
Here, we have the function ${{x}^{3}}$ and its domain is R, that is all real numbers. Drawing the graph of ${{x}^{3}}$ for the domain Q, that is the set of all rational numbers, we have,

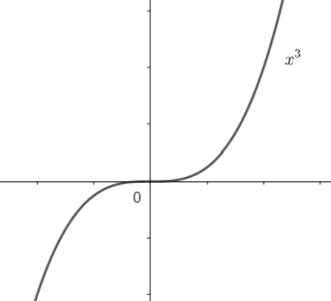
Here, from the graph, it looks like the range of ${{x}^{3}}$ is all real numbers but on observing the graph carefully we see that the domain should be R for this result. But we have been provided with the set of rational numbers (Q) in the domain, which means we will never get an irrational number as our range. So, our range will only be rational numbers and not all real numbers (R). Therefore, ${{x}^{3}}$ is not an onto function for the given domain.
On checking all the options we conclude that option (b) is the correct answer.

Note: One must not get confused in option (d) in which the given function is ${{x}^{3}}$. Here, the domain was not all real numbers but it was all rational numbers. So, we cannot get an irrational number in the range. For example: - We cannot choose $x=\sqrt{2}$ in the domain and hence we will never get $2\sqrt{2}$ in the range but we know that $2\sqrt{2}$ is a real number, so the range will never be all the real numbers.